1.电机的基本概念
电机是依据电磁感应定律和电磁力定律,由电路和磁路构成的能实现机电能量转换或信号传递与转换的装置。
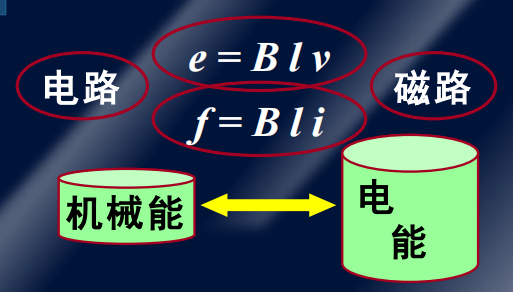
2.电机的分类
电机从运动方式上分为变压器和旋转电机,而旋转电机又分为直流和交流,交流电机分为异步和同步电机。
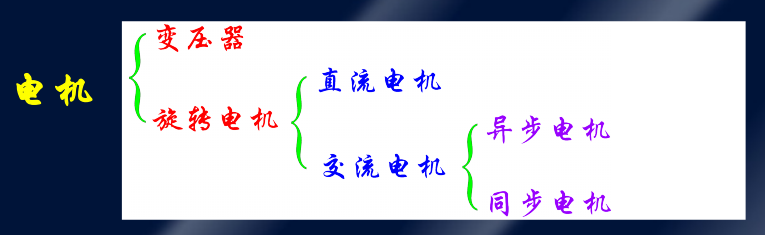
从功能上分类可以将电机分为电动机、发电机、变压器和控制电机。

3.电机的发展趋势
1)新型特种电机
新型特种电机是与科技最新发展联系最紧密、最富想象力、最具活力、也最具挑战性的学科分支。
2)基于计算机技术、电力电子技术、超导技术的发展
- 设计制造最优化
- 运行控制最优化(自动化、数字化、最优化)
- 高温超导技术应用
- 集成化、机电一体化
- 小型化、微型化
- 与高新技术融为一体
- 形成新的理论方法体系
4.铁磁材料特性
1)电机中使用的材料
① 导电材料:铜线。构成电路
② 导磁材料:硅钢片。构成磁路
③ 结构材料:铸铁、铸钢和钢板。承受力。
④ 绝缘材料:聚酯漆、环氧树脂、玻璃丝带等。用于导体之间和各类构件之间的绝缘处理。电机常用绝缘材料按性能划分为 A 、 E 、 B 、 F 、 H 、 C等 6 个等级。
2)铁磁材料的磁导率
磁导率是一个衡量物质对磁场的响应能力的物理量。在电磁学中,磁导率通常用来描述材料在磁场中的行为,类似于电导率用来描述材料在电场中的行为。磁导率通常用希腊字母$μ$表示
$$
\mu = B/ H
$$
- 铁磁材料的磁导率通常远远大于自由空间中的真空磁导率 $μ_0$,这表示铁磁材料对磁场的响应能力要更强。
- $μ_{Fe}$为非常数,随 $B $的变化而变化。
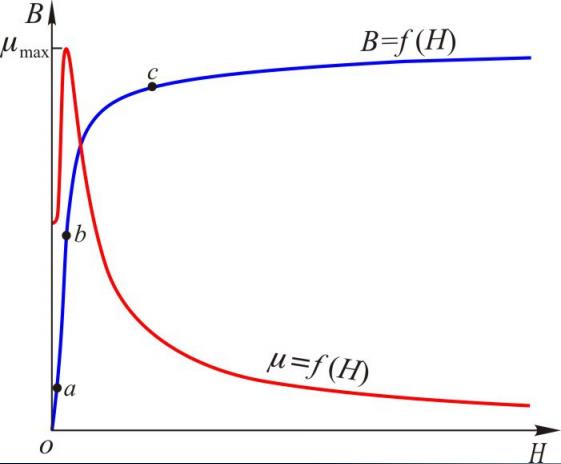
- 存在磁饱和现象:当铁磁材料中的磁感应强度$ B $达到一定程度后,材料会进入磁饱和状态。在磁饱和状态下,随着外加磁场强度 $H$ 的增加,磁感应强度 $B$ 的增加会逐渐减缓,这是因为材料的磁性已经接近饱和状态,难以进一步增强磁感应强度。因此,铁磁材料的磁导率 $μ_{Fe}$ 随着外加磁场强度$ H$ 的增加而减小,反映了这种磁饱和现象。
3)磁化曲线
当外部磁场 $H$ 作用在材料上时,磁感应强度 $ B$ 会发生变化,它们之间的关系可以表示为磁化曲线,记作 $B=f(H)$。
4)磁滞与磁滞损耗
铁磁材料中磁感应强度$B$的变化滞后于外部磁场强度$H$的变化的现象被称为磁滞。
如下图所示就是铁磁材料交变(循环)磁化过程中的磁滞回线。
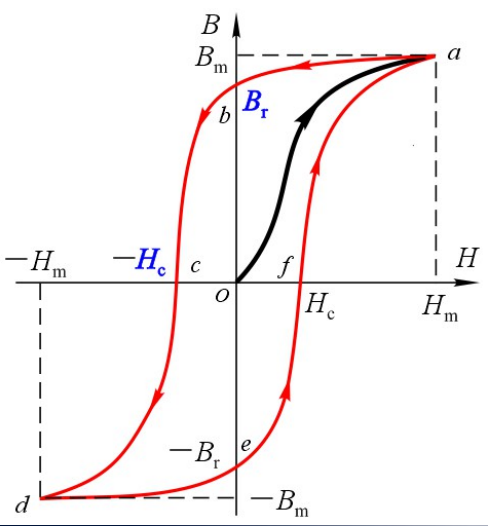
- 剩磁 $B_r$
- 矫顽力 $H_c$
- 软磁材料:磁滞回线很窄。硅钢片、铸铁、铸钢等。
- 硬磁材料:磁滞回线很宽,或叫永磁材料。常用的永磁材料有钐钴( SmCo)、钕铁硼( NdFeB )等。
基本磁化曲线
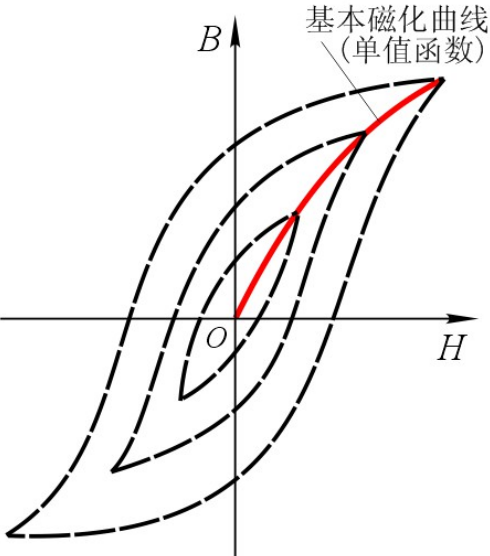
磁滞损耗:铁磁材料在交变磁场作用下的反复磁化过程中,磁畴会不停转动,相互之间会不断摩擦,因而就要消耗一定的能量,产生功率损耗。这种损耗称为磁滞损耗。
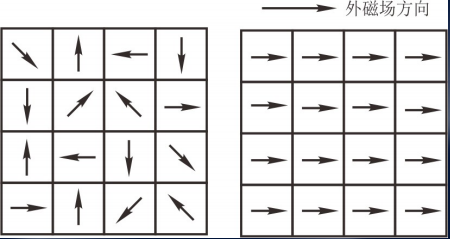
磁滞损耗(Hysteresis Loss)的大小与磁滞回线的面积、交变磁场频率 $f$ 和铁心体积 $V$ 成正比,这可以用如下表达式表示:
$$
P_h \propto A \cdot f \cdot V
$$
由于硅钢片的磁滞回线面积很小,而且导磁性能好。 因此,大多数电机、变压器或普通电器的铁心都采用。

5)涡流与涡流损耗
涡流是一种在铁磁材料中产生的感应电动势和电流的现象,在交变磁场中呈现涡旋状,因此被称为涡流。涡流在材料内部形成闭合回路,导致电流环流而产生损耗和能量耗散。
涡流损耗指的是涡流在其流通路径上的等效电阻中产生的 $I^2R$损耗,其中$I$ 为涡流产生的电流,$R$ 为等效电阻。这种损耗会导致能量转化为热,造成材料发热。
涡流损耗$P_w$ 与磁场交变频率 $ f$、材料厚度 $d$、最大磁感应强度 $B_m$ 和材料的电阻率 $ρ$成正比,可以用以下公式表示:
$$
P_w \propto \rho \cdot V \cdot f \cdot d^2 \cdot B_m^2
$$
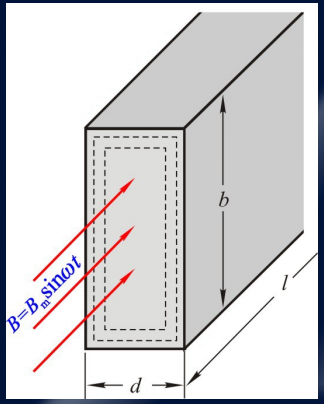
要减少涡流损耗,首先可以通过减小材料的厚度$ d$ 来降低损耗,其次可以增加涡流回路中的电阻,例如通过在电工钢片中添加适量的硅制成硅钢片,以显著提高电阻率$ρ$,从而减少涡流损耗。这对于设计和制造电机、变压器等设备非常重要,以提高设备的效率和性能。
6)铁耗
铁耗是指在铁磁材料中,由于交变磁场作用产生的磁滞损耗和涡流损耗的综合效应。
5.电机中的基本电磁定律
1)常用的物理量
磁通密度$B$ 单位:特斯拉$T$
磁通$Φ$ 单位韦伯$ Wb$
磁场强度$H$ 单位$A/m$
2)全电流定律
磁场强度沿任意的闭合路径的线积分等于闭合路径包围的导体电流的代数和。
电流是产生磁场的源
$$
\oint \mathbf{H} \cdot d\mathbf{l} = I
$$
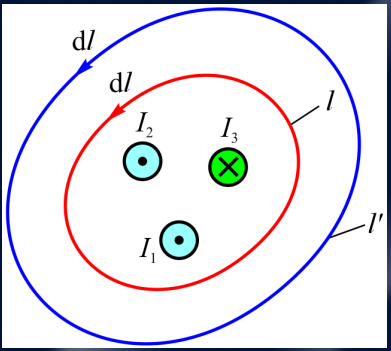
3)电磁感应定律
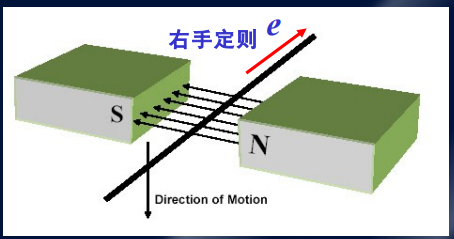
运动电动势
当描述运动电动势时,它通常与一个导体在磁场中运动时产生的感应电动势相关。运动电动势的一般公式可以表示为:
$$
\mathcal{E}_T = B \cdot l \cdot v
$$
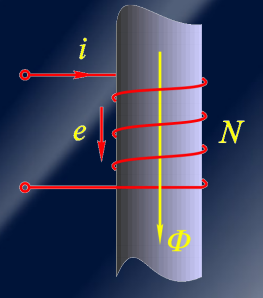
变压器电动势
对于变压器电动势,这通常涉及到一个变压器的电磁感应。对于一个理想的变压器,其次级绕组的电动势可以表示为:
$$
\mathcal{E}_V = -N \cdot \frac{d\Phi}{dt}
$$
当磁通按正弦规律变化时,感应电动势有效值为:
$$
e = -N \omega \Phi_m \cos(\omega t) = E_m \sin(\omega t - 90^\circ)
$$
感应电动势与磁通变化规律一致,滞后90度。
4)电磁力定律
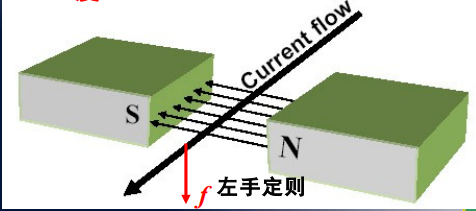
将长度为$l$的导体置于磁场$B$中,通入电流$i$,导体会受到力的作用,称为电磁力,其计算公式为:
$$
f = B \cdot l \cdot i
$$
式中,电磁力、磁场和载流导体的关系由左手定则确定。
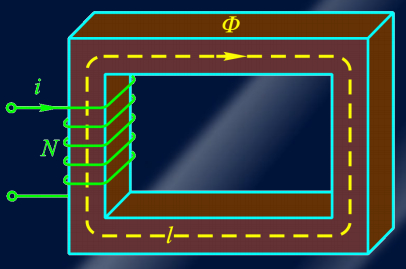
6.磁路基本定律及其计算方法
磁路的基本概念类似于电路,其中磁通被类比为电流,而磁阻和磁导率与电路中的电阻和电导率类似。
1)磁阻欧姆定律
根据磁路的欧姆定律,磁通(磁通量) $Φ$ 与磁势(磁动势) $F $之间的关系可以表示为:
$$
\Phi = \mathcal{F} \cdot R_m
$$
铁磁材料的磁阻随饱和程度的提高而增加,磁导随饱和程度的提高而减小。
2)磁路基尔霍夫第一定律
描述了磁通在封闭磁路中的守恒原理,类似于电路中的基尔霍夫第一定律。根据这一定律,通过任何封闭面的总磁通量的代数和等于零,或者说进入封闭面的磁通量等于从该封闭面穿出的磁通量。数学表达如下:
$$
\Sigma \Phi = 0
$$
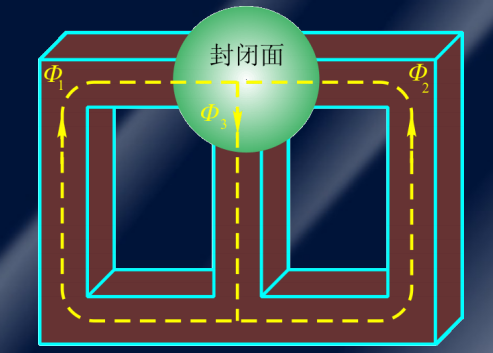
3)磁路基尔霍夫第二定律
描述了在一个封闭磁路中,沿着任意闭合路径的磁势 $F $与通过该路径的电流 $i$ 之间的关系。该定律可以根据麦克斯韦方程组的积分形式推导得出。
根据磁路基尔霍夫第二定律,对于任意封闭路径,有以下等式:
$$
\sum N_i \cdot i_i = \sum H_i \cdot l_i = \sum \Phi \cdot R_m
$$
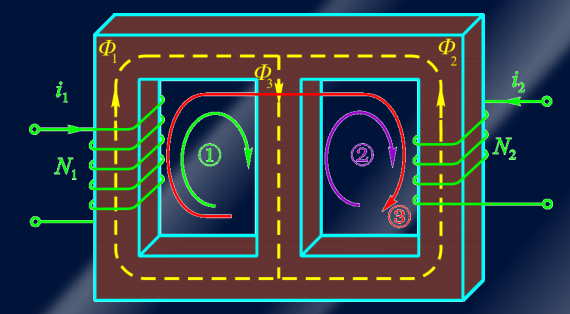
以上等式强调了磁路中的电流、磁场强度、磁通和磁阻之间的关系,即在封闭路径中,磁势的代数和等于通过该路径的电流乘以其绕组匝数之和,同时也等于磁场强度与路径长度之积之和,还等于通过路径的磁通乘以路径的磁阻之和。
4)磁路和电路的类比关系
| 特性/方面 | 电路 | 磁路 |
|---|---|---|
| 物理量 | 电流 ($I$) | 磁通 ($Φ$) |
| 类比关系 | 电流传递能量,产生电场 | 磁通传递能量,产生磁场 |
| 单位 | 安培($A$) | 韦伯($Wb$) |
| 欧姆定律 | $V = I \cdot R$ | $\mathcal{F} = \Phi \cdot R_m$ |
| 等效电阻/磁阻 | 串/并联电阻:$R_{\text{eq}} = R_1 + R_2$ | 串/并联磁阻:$R{m,eq} = R{m1} + R_{m2}$ |
| 电流流向 | 电流从高电势到低电势流动 | 磁通从高磁势到低磁势流动 |
| 欧姆定律推导 | $V = I \cdot R$ | $ \mathcal{F} = \Phi \cdot R_m$ |
| 基尔霍夫定律 | $ΣI = 0$(节点定律) | $ΣΦ = 0$ (磁路基尔霍夫第一定律) |
| $ΣV = 0$(环路定律) | $ΣN \cdot i = ΣH \cdot l = ΣΦ \cdot R_m$ (磁路基尔霍夫第二定律) |
7.磁路计算方法
在磁路计算中,通常会遇到以下两类问题:
- 第一类问题:已知磁通$Φ$,求解磁动势 $F$。
- 第二类问题:已知磁动势 $F$,求解磁通 $Φ$。
在电机和变压器设计等领域的磁路计算中,常常涉及第一类问题。而对于第二类问题,一般需要使用迭代法进行求解,这种计算往往由计算机来完成。
磁路计算中的欧姆定律是描述磁路中磁通、磁动势和磁阻之间关系的类比法则,类似于电路中的欧姆定律。根据磁路欧姆定律,磁动势$F$ 与磁通$Φ $之间的关系可以表示为:
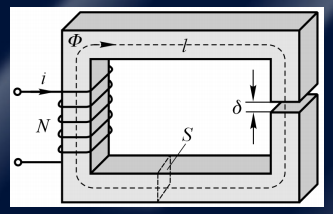
自感和互感
自感
$$
L = N^2 \cdot \mu \cdot A
$$
- 自感的大小与匝数的平方和磁路的磁导率成正比。
- 铁心线圈的自感要比空心线圈的大得多,这是因为铁心可以集中磁场并增加自感。
- 铁心线圈的电感不是常数,当磁路饱和程度增加时,自感会下降。磁路饱和会影响磁通量和磁动势之间的关系,从而影响自感的大小。
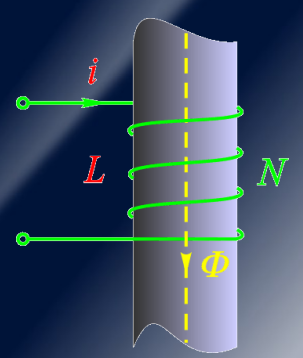
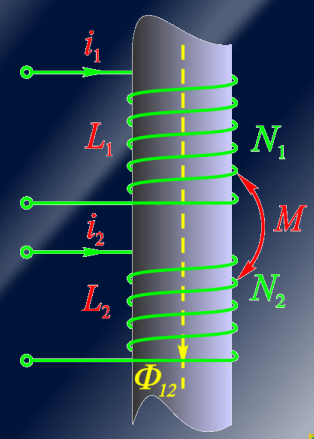
互感
互感描述了两个线圈之间的耦合效应,其中线圈之间的匝数乘积和互感磁通所经过的磁路的磁导率成正比。
$$
M = k \cdot \sqrt{N_1 \cdot N_2}
$$
参考
1、《电机学第四版》 华中科技大学出版社 辜承林