机器学习与神经网络学习笔记

这几天在看吴恩达的深度学习视频，记不清已经是第几次捡起来了，之前每次都没看完，希望在正式上班之前把这部分看完吧

神经网络基础

神经网络是深度学习的基本组成部分。它由多个神经元和层级组成，每个神经元通过激活函数对输入进行处理，并将输出传递给下一层。神经网络通过学习权重和偏置来逼近目标函数。

下图是一个简单的逻辑回归模型，首先需要输入特征$x$，通过特征$W$和$b$计算出$z$，接下来使用$𝑧$就可以计算出$𝑎$，然后可以计算 出 loss function 𝐿(𝑎, 𝑦)

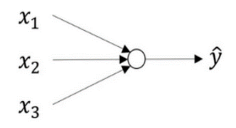
神经网络看起来是如下这个样子。可以把许多 sigmoid 单元堆叠起来形成一个神经网络。它包含了之前讲的计算的 两个步骤：首先计算出值𝑧，然后通过𝜎(𝑧) 计算值𝑎。

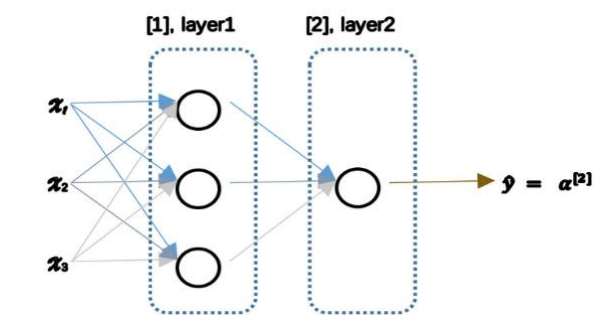
在这个神经网络对应的 3 个节点，首先计算第一层网络中的各个节点相关的数𝑧 [1]，接着计算𝛼 [1]，在计算下一层网络同理； 我们会使用符号 [𝑚] 表示第𝑚层网络中 节点相关的数，这些节点的集合被称为第𝑚层网络。

我们有输入特征𝑥1、𝑥2、𝑥3，它们被竖直地堆叠起来，这叫做神经网络的输入层。它包含了神经网络的输入；然后这里有另外一层我们称之为隐藏层（图中的四个结点），最后一层只由一个结点构成，而这个只 有一个结点的层被称为输出层，它负责产生预测值。解释隐藏层的含义：在一个神经网络中， 当你使用监督学习训练它的时候，训练集包含了输入𝑥也包含了目标输出𝑦，所以术语隐藏层 的含义是在训练集中，这些中间结点的准确值我们是不知道到的，也就是说你看不见它们在 训练集中应具有的值。你能看见输入的值，你也能看见输出的值，但是隐藏层中的东西，在训练集中你是无法看到的。所以这也解释了词语隐藏层，只是表示你无法在训练集中看到他 们。

神经元模型是神经网络中的基本单元，它接收输入信号并通过激活函数进行非线性变换。

• 输入$A$：神经元接收来自上一层的输入信号。
• 权重$W$：每个输入信号都与一个权重相关联，权重决定了输入对神经元的影响程度。
• 偏置$b$：每个神经元还有一个偏置，它相当于一个常数项，可以调整神经元的输出。

神经网络的训练通常涉及以下步骤：

1. 数据准备：收集和准备用于训练神经网络的数据集。这包括对数据进行清洗、划分训练集和测试集，并进行必要的预处理步骤，例如标准化或归一化。
2. 定义网络结构：确定神经网络的结构，包括层数、每层的神经元数量以及激活函数的选择。这些决定将根据特定问题和数据集的需求进行调整。
3. 参数初始化：初始化神经网络的参数，例如权重和偏置项。常见的初始化方法包括零初始化、随机初始化和 He 初始化等。
4. 前向传播：执行前向传播算法，将输入数据通过神经网络进行推理，计算每一层的激活值（输出）。
5. 计算损失：使用定义的损失函数（例如交叉熵损失）计算预测结果与真实标签之间的差异，衡量模型的性能。
6. 反向传播：通过反向传播算法计算每一层的梯度，根据损失函数的梯度信息更新参数，以便减少损失。
7. 参数更新：根据反向传播计算得到的梯度信息，使用优化算法（如梯度下降）更新神经网络的参数。
8. 重复迭代：重复执行步骤 4 到步骤 7，直到达到指定的训练迭代次数或满足停止条件。
9. 模型评估：使用测试集或交叉验证集对训练后的神经网络进行评估，计算准确率、精确率、召回率等指标，评估模型的性能。
10. 预测：使用训练好的神经网络对新的未见过的数据进行预测。

参数初始化

当你训练神经网络时，权重随机初始化是很重要的。对于逻辑回归，把权重初始化为 0 当然也是可以的。但是对于一个神经网络，如果你把权重或者参数都初始化为 0，那么梯度下降将不会起作用。因此，一般把$W$初 始化为很小的随机数。然后$𝑏$没有这个对称的问题（叫做 symmetry breaking problem），所以可以把$𝑏$初始化为 0。

def initialize_parameters_random(layers_dims):
    parameters = {}
    L = len(layers_dims) - 1  # 网络层数
 
    for l in range(1, L + 1):
        parameters[f"W{l}"] = np.random.randn(layers_dims[l], layers_dims[l-1]) * 0.01
        parameters[f"b{l}"] = np.zeros((layers_dims[l], 1))
 
    return parameters
 

				

					
				
				

					
				
				

					
				
				

					
				
			

前向传播

神经网络的前向传播过程是从输入层到输出层的计算过程。对于每一层，输入经过权重和偏置的线性变换，然后通过激活函数进行非线性变换，得到输出。

计算流程

前向传播的计算流程为：

$Z^{[1]} = W^{[1]}X + b^{[1]}$

$A^{[1]} = g^{[1]}(Z^{[1]})$

$Z^{[2]} = W^{[2]}A^{[1]} + b^{[2]}$

$A^{[2]} = g^{[2]}(Z^{[2]})$

...

$Z^{[L-1]} = W^{[L-1]}A^{[L-2]} + b^{[L-1]}$

$A^{[L-1]} = g^{[L-1]}(Z^{[L-1]})$

$Z^{[L]} = W^{[L]}A^{[L-1]} + b^{[L]}$

$A^{[L]} = g^{[L]}(Z^{[L]})$

其中，$X$ 表示输入数据，$A^{[l]}$ 表示第 l 层的输出，$W^{[l]}$ 和 $b^{[l]}$ 分别表示第 l 层的权重和偏置，$g^{[l]}$ 表示第 l 层的激活函数。

激活函数

激活函数引入了非线性特性，使神经网络能够学习复杂的非线性关系。常见的激活函数有 sigmoid 函数、ReLU 函数和 tanh 函数。

sigmoid 函数

tanh 激活函数

ReLU 函数

 

sigmoid 激活函数：除了输出层是一个二分类问题基本不会用它。

tanh 激活函数：tanh 是非常优秀的，几乎适合所有场合。

ReLu 激活函数：最常用的默认函数，如果不确定用哪个激活函数，就使用 ReLu 或者 Leaky ReLu。

代码实现

• 在以下代码中，forward_propagation 函数接受输入特征数据 X 和包含参数的字典 parameters 作为输入，执行 n 层神经网络的前向传播计算。
• 根据网络的层数 L，依次从参数字典中提取权重矩阵和偏置向量，并根据前向传播的计算公式，计算每一层的加权输入 Z 和激活值 A。
• 中间计算结果以元组形式保存在 caches 列表中，用于后续的后向传播计算。
• 最后，返回输出层的激活值 AL 和中间计算结果的缓存 caches。这些结果可以用于损失计算和反向传播过程。

def forward_propagation(X, parameters):
    """
    前向传播计算
 
    参数：
    X - 输入特征数据，维度为（特征数量，样本数量）
    parameters - 包含参数的字典，参数命名规则为"Wl"和"bl"，表示第l层的权重矩阵和偏置向量
 
    返回：
    AL - 输出层的激活值
    caches - 包含每一层的中间计算结果的字典列表，用于后向传播
    """
 
    L = len(parameters) // 2  # 神经网络的层数
    caches = []
    A = X
 
    # 前L-1层的前向传播（使用ReLU激活函数）
    for l in range(1, L):
        W = parameters['W' + str(l)]
        b = parameters['b' + str(l)]
        Z = np.dot(W, A) + b
        A = relu(Z)
        cache = (Z, A)
        caches.append(cache)
 
    # 输出层的前向传播（使用Sigmoid激活函数）
    WL = parameters['W' + str(L)]
    bL = parameters['b' + str(L)]
    ZL = np.dot(WL, A) + bL
    AL = sigmoid(ZL)
    cacheL = (ZL, AL)
    caches.append(cacheL)
 
    return AL, caches

				

					
				
				

					
				
				

					
				
				

					
				
			

损失函数

计算损失函数是深度学习中的重要步骤，它用于衡量模型的预测结果与实际标签之间的差异。损失函数的作用是量化模型的预测误差，并通过最小化损失函数来优化模型的参数。

在分类问题中，常用的损失函数是交叉熵损失函数（Cross Entropy Loss）。交叉熵损失函数可以有效地衡量两个概率分布之间的差异，用于衡量模型的输出与实际标签之间的差异。常见的损失函数有均方误差损失函数和交叉熵损失函数。对于二分类问题，交叉熵损失函数的计算公式如下：

• 均方误差损失函数公式：

 

• 交叉熵损失函数公式：

代码实现

def compute_loss(AL, Y):
    """
    计算交叉熵损失函数
 
    参数：
    AL - 输出层的激活值，维度为（1，样本数量）
    Y - 实际标签，维度为（1，样本数量）
 
    返回：
    loss - 交叉熵损失
    """
    m = Y.shape[1]  # 样本数量
 
    # 计算交叉熵损失
    loss = -1 / m * np.sum(Y * np.log(AL) + (1 - Y) * np.log(1 - AL))
 
    return loss
 

				

					
				
				

					
				
				

					
				
				

					
				
			

以上代码中，compute_loss 函数接受输出层的激活值 AL 和实际标签 Y 作为输入，通过交叉熵损失函数的计算公式，计算出交叉熵损失值。最后，返回计算得到的交叉熵损失值 loss。

反向传播

反向传播是神经网络中的一种训练算法，通过计算梯度来更新权重和偏置。它利用链式法则将误差从输出层传播回输入层，并根据梯度下降算法更新模型参数。

反向传播的计算流程为：

$dZ^{[L]} = A^{[L]} - Y$

$dW^{[L]} = \frac{1}{m} dZ^{[L]} A^{[L-1]T}$

$db^{[L]} = \frac{1}{m} \sum dZ^{[L]}$

$dZ^{[L-1]} = W^{[L]T} dZ^{[L]} * g^{[L-1]'}(Z^{[L-1]})$

$dW^{[L-1]} = \frac{1}{m} dZ^{[L-1]} A^{[L-2]T}$

$db^{[L-1]} = \frac{1}{m} \sum dZ^{[L-1]}$

...

$dZ^{[1]} = W^{[2]T} dZ^{[2]} * g^{[1]'}(Z^{[1]})$

$dW^{[1]} = \frac{1}{m} dZ^{[1]} X^T$

$db^{[1]} = \frac{1}{m} \sum dZ^{[1]}$

其中，$dZ^{[l]}$ 表示第 l 层的梯度，$dW^{[l]}$ 和 $db^{[l]}$ 分别表示第 l 层的权重和偏置的梯度，$g^{[l]'}$ 表示第 l 层激活函数的导数，$W^{[l]}$ 表示第 l 层的权重。

代码实现

def backward_propagation(AL, Y, caches):
    """
    N层神经网络的反向传播
 
    参数：
    AL - 神经网络的输出，维度为（输出层大小，样本数量）
    Y - 实际标签，维度为（输出层大小，样本数量）
    caches - 包含前向传播过程中的缓存值的列表
 
    返回：
    grads - 包含模型参数相对于损失函数的梯度的字典
    """
    grads = {}
    L = len(caches)  # 网络层数
    m = AL.shape[1]  # 样本数量
    Y = Y.reshape(AL.shape)  # 保证Y和AL维度相同
 
    # 计算输出层的梯度
    dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
 
    # 反向传播
    current_cache = caches[L - 1]  # 最后一层的缓存值
    grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, activation="sigmoid")
 
    # 从倒数第二层开始反向传播
    for l in reversed(range(L - 1)):
        current_cache = caches[l]  # 当前层的缓存值
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)], current_cache, activation="relu")
        grads["dA" + str(l + 1)] = dA_prev_temp
        grads["dW" + str(l + 1)] = dW_temp
        grads["db" + str(l + 1)] = db_temp
 
    return grads
 

				

					
				
				

					
				
				

					
				
				

					
				
			

在上述代码中，backward_propagation 函数接受神经网络的输出 AL、实际标签 Y 和前向传播过程中的缓存值 caches 作为输入。根据反向传播的计算公式，首先计算输出层的梯度 dAL，然后从最后一层开始，依次进行反向传播，计算每一层的梯度 dA_prev、dW 和 db。其中，linear_activation_backward 函数用于计算每一层的线性部分和激活函数的梯度。

最后，将计算得到的梯度保存到字典 grads 中并返回。这些梯度可以用于更新模型的参数。通过反向传播，梯度会从输出层逐渐传播回输入层，从而计算模型参数的梯度。

参数更新

在神经网络中，通常使用梯度下降法来更新参数。

其中，$\theta$表示参数，$\alpha$表示学习率，$\nabla J(\theta)$表示损失函数$J(\theta)$关于参数$\theta$的梯度。

代码实现

def update_parameters(parameters, grads, learning_rate):
    """
    使用梯度下降更新模型参数
 
    参数：
    parameters - 包含模型参数的字典
    grads - 包含模型参数相对于损失函数的梯度的字典
    learning_rate - 学习率
 
    返回：
    parameters - 更新后的模型参数字典
    """
    L = len(parameters) // 2  # 网络层数
 
    # 更新每一层的参数
    for l in range(L):
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]
 
    return parameters
 

				

					
				
				

					
				
				

					
				
				

					
				
			

在上述代码中，update_parameters 函数接受模型的参数字典 parameters、模型参数相对于损失函数的梯度字典 grads 和学习率 learning_rate 作为输入。根据梯度下降的更新规则，对每一层的参数进行更新。

通过循环遍历每一层，更新参数 W 和 b。更新公式为 parameter = parameter - learning_rate * gradient，其中 parameter 表示参数，learning_rate 表示学习率，gradient 表示对应的梯度。

最后，返回更新后的模型参数字典 parameters。这些更新后的参数可以用于下一轮的前向传播和反向传播过程。

参数更新是神经网络训练的关键步骤，通过不断更新参数，使模型逐渐优化，减小损失函数，提高预测准确率。学习率 learning_rate 控制着每次更新的步长，需要合适的学习率来保证模型能够收敛到最优解。

构建深层神经网络模型

layers_dims = [12288, 20, 7, 5, 1] #  5-layer model
def L_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False):
    """
    实现一个L层神经网络模型的训练
 
    参数：
    X - 输入特征数据，维度为 (输入特征数, 样本数)
    Y - 标签数据，维度为 (1, 样本数)
    layers_dims - 列表，包含输入层、隐藏层和输出层的神经元数量
    learning_rate - 学习率
    num_iterations - 迭代次数
    print_cost - 是否打印成本值
 
    返回：
    parameters - 训练后的模型参数
    """
    np.random.seed(1)
    costs = []  # 用于保存成本值
 
    # 初始化参数
    parameters = initialize_parameters_random(layers_dims)
 
    # 迭代训练
    for i in range(num_iterations):
        # 前向传播
        AL, caches = forward_propagation(X, parameters)
 
        # 计算成本
        cost = compute_loss(AL, Y)
 
        # 反向传播
        grads = backward_propagation(AL, Y, caches)
 
        # 参数更新
        parameters = update_parameters(parameters, grads, learning_rate)
 
        # 打印成本值
        if print_cost and i % 100 == 0:
            print("Cost after iteration {}: {}".format(i, cost))
        if i % 100 == 0:
            costs.append(cost)
 
    # 绘制成本曲线
    plt.plot(np.squeeze(costs))
    plt.ylabel('Cost')
    plt.xlabel('Iterations (per tens)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()
 
    return parameters
 
parameters = L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True)#训练模型
pred_train = predict(train_x, train_y, parameters)#训练集验证
pred_test = predict(test_x, test_y, parameters)#测试集验证

				

					
				
				

					
				
				

					
				
				

					
				
			

该函数接受输入特征数据 X，标签数据 Y，神经网络层的维度 layers_dims，学习率 learning_rate，迭代次数 num_iterations 和是否打印成本值 print_cost 作为参数。

函数首先初始化模型的参数，然后通过迭代训练的方式进行模型优化。在每次迭代中，函数执行以下步骤：

1. 前向传播：通过调用 L_model_forward 函数实现，计算预测值 AL 和缓存值 caches。
2. 计算成本：通过调用 compute_cost 函数实现，计算模型的损失函数成本。
3. 反向传播：通过调用 L_model_backward 函数实现，计算模型参数相对于损失函数的梯度。
4. 参数更新：通过调用 update_parameters 函数实现，根据梯度下降的更新规则更新模型的参数。
5. 打印成本值：根据设定的条件，打印每一百次迭代的成本值。
6. 绘制成本

这样就完成了深度神经网络的构建。

学习视频：https://www.coursera.org/deeplearning-ai

笔记资料：fengdu78/deeplearning_ai_books: deeplearning.ai（吴恩达老师的深度学习课程笔记及资源） (github.com)