title: "谱聚类算法"
date: 2023-04-23
categories:
- [学习记录,机器学习]
tags: - 机器学习
- 聚类算法
谱聚类算法:谱指的是某个矩阵的特征值。
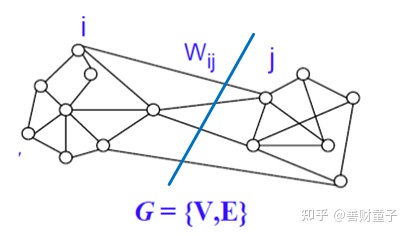
谱聚类的思想来源于图论,它把待聚类的数据集中的每一个样本看做是图中一个顶点,这些顶点连接在一起,连接的这些边上有权重,权重的大小表示这些样本之间的相似程度。同一类的顶点它们的相似程度很高,在图论中体现为同一类的顶点中连接它们的边的权重很大;不在同一类的顶点连接它们的边的权重很小。于是谱聚类的最终目标就是找到一种切割图的方法,使得切割之后的各个子图内的权重很大,子图之间的权重很小。
一、预备知识
-
假设给定一个数据集$X={ x_1,x_2,...,x_n }$,我们将这个n个数据向量当做m维空间中某一幅无向图上的一个个点,目的是衡量这些点的相似性。
-
把图叫做相似图,记为$G=(V,E)$,其中$V={ v_1,v_2...,v_n }$表示顶点,$E$表示边的集合。两个顶点$v_i,vj$的边的权重记为$\omega{ij}$
-
相似性用$s_{ij}$表示,越大表示越相似
-
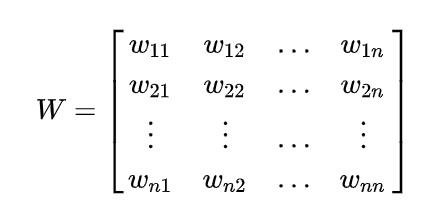
n个权重点构成一个矩阵$W=(\omega_{ij})$
1.1邻接矩阵、度和度矩阵、连通子图
(1)邻接矩阵
所有顶点之间的权重构成一个矩阵,叫邻接矩阵,也叫权重矩阵。两个顶点互相之间的权重是一样的,因此$W$是对称矩阵。
(2)度矩阵
对于某个顶点的度$d_i,i=1,2,...,n$,定义为
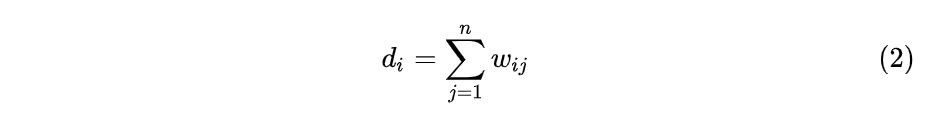
度其实就是邻接矩阵的第$i$行的和。(因为邻接矩阵是对称矩阵,所以第$j$列的和也可以)
度矩阵定义为$n$个度构成的对角矩阵:

对于给定顶点$V$的一个子集$A\subset V$,定义它的补为$\bar{A}$。对于某个顶点$v_i \in A$,定义对应的指示向量为$1_A = [f_1,f_2...,f_n]^T \in R^n$,若$v_i \in A$,则指示向量第i个位置为1,即$f_i = 1$,否则为0;对于两个子集A和B,我们定义:
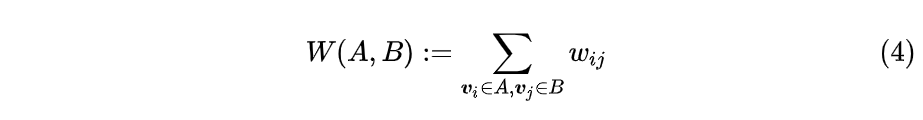
公式(4)表示两个子集中顶点之间的权重之和,注意这里不包含子集内顶点之间的权重。
子集大小有两种定义

(3)连通子图
如果$A$中的任意两个顶点都至少存在一条路径将他们连接起来,并且$A$中其他顶点也在这条路径上,则$A$是连接的。如果子集$A$是连接的,并且与他的补$\bar{A}$不存在任何的连接,则称为连通子图。非空子集$A_1,A_2,...,A_k$构成$V$的一个分割,即$A_1\cup A_2 \cup... \cup A_k=V$
1.2 相似图的衡量方法
如果度量空间具有距离越远越不相似,越近越相似的特性,通常作为相似度的衡量标准。
(1)$ \epsilon - 近邻法 $
采用欧式距离计算两个顶点的距离$s_{ij}$,然后设定一个阈值$\epsilon$
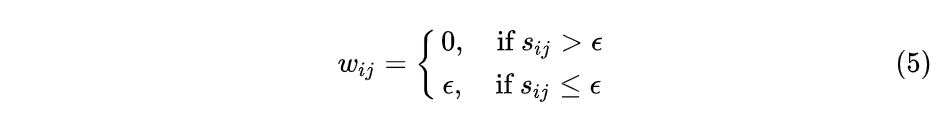
(2)k-邻近法
利用KNN算法遍历所有的样本点,取每个样本最近的k个点作为近邻,取与顶点最近的$k$个顶点,该顶点与$k$个顶点的权重都大于0。但是这种方法不能保证相似矩阵是对称的,因为两个顶点可能不是在互相的近邻中。一般使用两种方法保证相似矩阵的对称。
- 两个顶点只要其中一个点在另一个顶点的近邻中,则令$\omega{ij}=\omega{ji}$

- 两个顶点同时在双方的近邻中,则令$\omega{ij}=\omega{ji}$,否则$\omega{ij}=\omega{ji}=0$
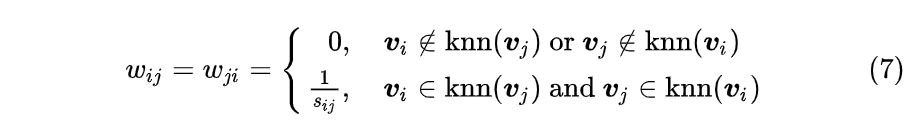
(3)全连接法
该方法将所有的顶点都连接起来。然后通过度量空间中某种对称度量算子来计算顶点之间的相似度。常用的有多项式核函数,高斯核函数和Sigmoid核函数。最常用的是高斯核函数RBF,此时相似矩阵和邻接矩阵相同,比如使用高斯核函数计算两个顶点之间的相似度:
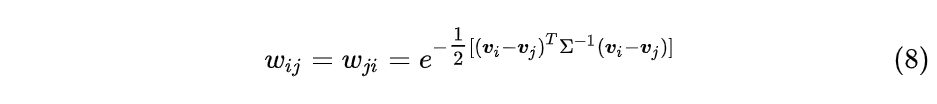
实际应用中,使用全连接法是最普遍的,而在全连接法中使用高斯径向核RBF是最普遍的。
1.3 图拉普拉斯矩阵
1.3.1 非规范化的图拉普拉斯矩阵
图拉普拉斯矩阵的定义如下:
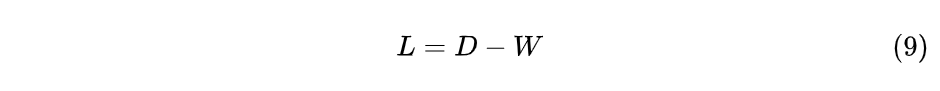
其中$D$为度矩阵,W为权重(近似)矩阵,所以L也是对称矩阵
性质:
- 对于任意向量$f \in R^n $
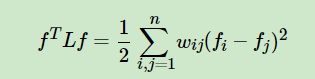
-
$L$是一个对称半正定矩阵。
-
$L$的最小特征值为0,对应的特征向量是全为1的向量$1$。$0 \le \lambda_1 \le \lambda_2 ...\le \lambda_n$
-
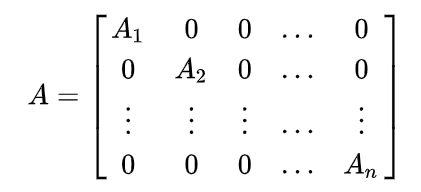
对于一个对角分块矩阵$A$
他的特征值等于各个分块矩阵的特征值。
-
若$G$是一个具有非负权重的无向图,则它对应的图拉普拉斯矩阵L的0特征值的代数重数k等于G中连通子图的个数,假设k个连通子图记为$A_1,A_2,...Ak$,并且0特征值对应的特征值空间由各个连通子图的指示向量$1{A_i} \in R_n$。
1.3.2规范化的图拉普拉斯矩阵
有两种规范化的图拉普拉斯矩阵,他们互相联系。这两种规划化的图拉普拉斯矩阵定义为:
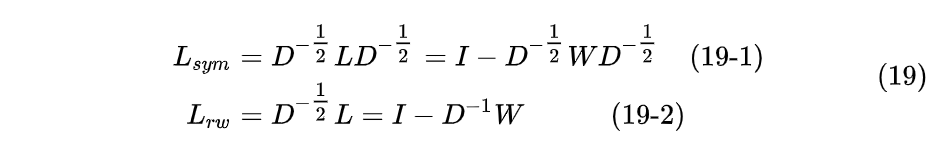
公式(19)中的$L{sym}$是一个对称矩阵,下标sym是单词symmetric的简写,$L{rw}$不是对称矩阵,该矩阵和随机游走(random walk)相关,下标rw就是random walk 的首字母组合。
$L_{sym}$的性质:
- 对于任意向量$f \in R^n$


-
$L{sym}$和$L{rw}$具有相同的特征值,对应的特征值向量关系为
$$
\omega = D^{1/2} u
$$
二、切割方法
优化的目标函数为:
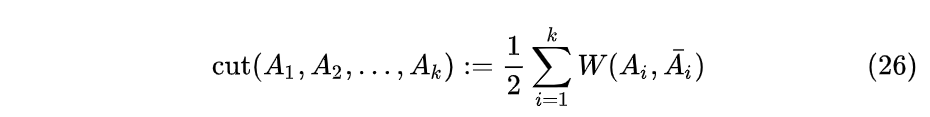
2.1 RatioCut切图
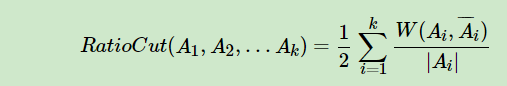
引入指示向量$h_j∈{h_1,h_2,..h_k},j=1,2,...k,$对于任意一个向量$h_j$, 它是一个n维向量(n为样本数),我们定义
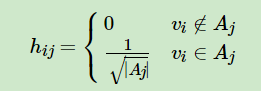
对应的RatioCut函数表达式为:
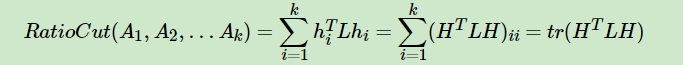
松弛化的目标函数:
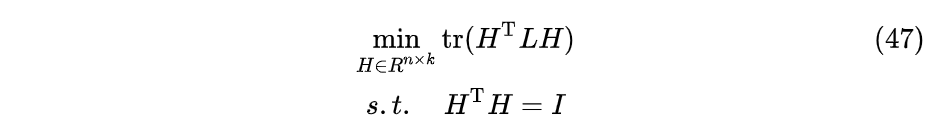
将图切割为k个分组的问题转换成了求图拉普拉斯矩阵L的前k个最小特征值对应的特征向量$h_j∈{h_1,h_2,..h_k},j=1,2,...k,$和L二次型之和。
求出来的$h_i$并不能准确指示顶点所属类别,将矩阵$H= [h_1,h_2,..h_k]$当作一个新的具有k个维度特征n个样本的数据集进行$k-means$聚类。是对每一个样本聚类,聚类的类别数是k,也就是对H的每一行进行聚类。
2.2 Ncut切图
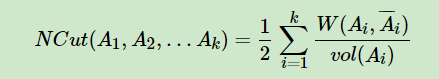
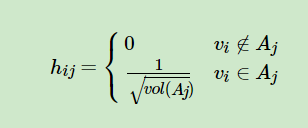
优化目标任然是
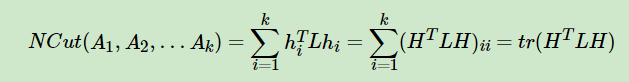
松弛化的目标函数:
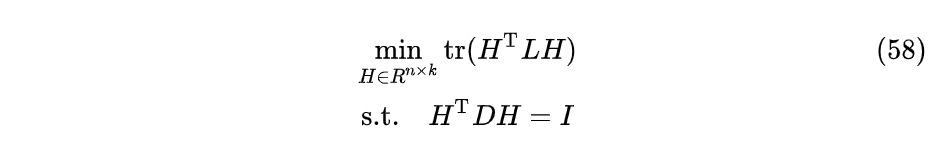
令$B= D^{1/2}H$:
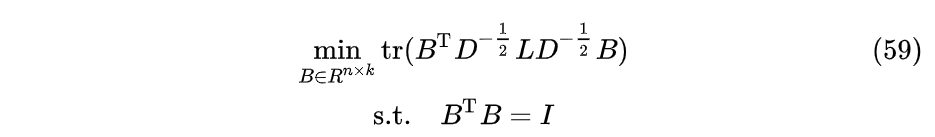
上式的解$B^$也就是矩阵$L_{sym}$的前k个最小特征值对应的特征向量按列排列成$B^ = { b_1,b_2,...,bk }$。反带入可得$L{rw}$前k个最小特征值对应的特征向量$H={h_1,h_2,..h_k}$
或者矩阵$L$的前$k$个最小的广义特征值对应的特征向量。
三、算法实现步骤
最常用的相似矩阵的生成方式是基于高斯核距离的全连接方式,最常用的切图方式是Ncut。而到最后常用的聚类方法为K-Means。
假设聚成$k$个分组
(1)计算相似度矩阵$W$
(2)计算度矩阵$D$
(3)计算图拉普拉斯矩阵$L$,构建标准化后的图拉普拉斯矩阵$D^{-1/2}LD^{-1/2}$
(4)直接对$D^{-1/2}LD^{-1/2}$进行特征值分解,获取其前$k$个特征值对应的特征向量按照列排成矩阵$Q=[q_1,q_2,...,q_k]$
(5)对矩阵$Q$的 所有行$r_1,r_2,...r_n$标准化,组成$n*k$进行聚类,如使用$k-means$方法或者别的方法进行聚类得到$C_1,C_2,...,C_k$
(6)输出原始数据的分组$A_1,A_2,...,A_k$,其中$A_i={v_j|r_j \in C_i }$
注意:在第(4)步也可以再计算规范化的矩阵$L_{sym}$,在对这个矩阵做特征分解或者做广义特征值分解,后面步骤相同。