一、机器人学

1.POE

（1）绪论

（2）形位空间

（3）刚体运动

3.1旋转与角速度

1.旋转矩阵

$$
R=Rot(\hat{\omega},\theta)
$$

满足以下条件

• 正则条件
• 正交条件
• 坐标系三个坐标轴遵循右手定则

3*3旋转矩阵组成的集合被称为特殊正交群SO(3)

特性

• 封闭性
• 结合律
• 幺元性
• 可逆性

用途

1. 表示姿态
2. 进行坐标系转换
3. 对向量和坐标系进行旋转变换

左乘旋转矩阵会得到绕固定坐标系中的转轴转动，右乘会得到绕物体坐标系中转轴的转动。

2.角速度

$$
\omega=\hat{\omega}\dot{\theta}
$$

反对称矩阵

在空间坐标系中的角速度

$$
[\omega_s]=\dot{R}R^{-1}
$$
物体坐标系下的角速度
$$
[\omega_b]=R^{-1}\dot{R}
$$
$\omega \in R^3$是角速度的向量表达形式，$[\omega]\in so(3)$是3*3矩阵表示形式。

3.转动的指数坐标表示

转动的三参数指数坐标

向量$\dot\omega \theta \in R^3$就是转动的三参数指数坐标形式，单独写就是转动的轴-角表示法

刚体转动的指数坐标

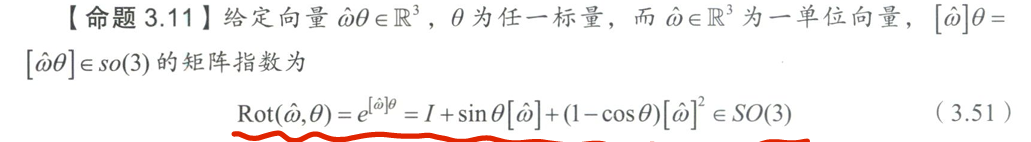
刚体转动的矩阵对数

若$\dot\omega \theta \in R^3$表示旋转矩阵R的指数坐标，那么反对称矩阵$[\hat{\omega }\theta]=[\hat{\omega }]\theta \in so(3)$就是矩阵R的矩阵对数。矩阵对数是矩阵指数的可逆形式。正像矩阵指数是矩阵形式的角速度$[\hat{\omega }]\theta \in so(3)$在单位时间（ 1秒）内的定积分，使刚体运动到给定姿态$R\in SO(3)$—样，矩阵对数则是对R进行微分，以找到一个常值角速度$[\hat{\omega }]\theta \in so(3)$的矩阵表示形式。

3.2刚体运动与运动旋量

齐次变换矩阵T与旋转矩阵R相对应，螺旋轴S与旋转轴$\hat\omega$相对应，运动旋量V(可表示成$S\dot\theta$）与角速度$[\hat{\omega }\theta]=[\hat{\omega }]\theta \in so(3)$相对应，而用于描述刚体位移的指数坐标$S\theta \in R^6$与刚体转动的指数坐标$\hat \omega \theta \in R^3$相对应。

特殊欧氏群SE(3)亦称刚体运动群或齐次变换矩阵群，是所有4×4实矩阵T的集合 。

运动旋量

将$\omega_b、v_b$合在一起组成一个六维向量形式。为此定义为物体坐标系中的速度，简称为物体运动旋量。

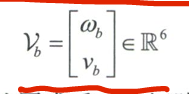
如前所述，角速度可以很方便的写成反对称矩阵形式，同样，运动旋量也能写成矩阵形式。

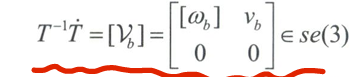
同样，基于空间坐标系，写出空间运动旋量

物体运动旋量和空间运动旋量的关系

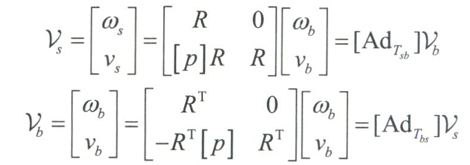
运动旋量的螺旋释义

运动旋量$V$也可以写成螺旋轴$S$与绕该轴转动的速度$\dot\theta$组合形式

$S=(\omega,v)$的矩阵表达式为

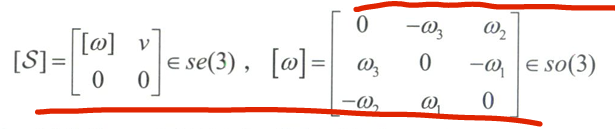
3.3刚体运动的指数坐标表达

Chasles_Mozzi定理:任何刚体运动都可通过绕空间某—固定螺旋轴S的运动来实现 。

类似转动情况，定义矩阵指数和矩阵对数

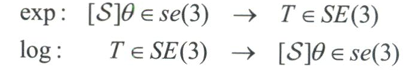
将矩阵指数进行级数展开

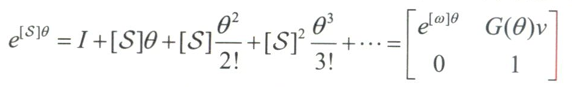
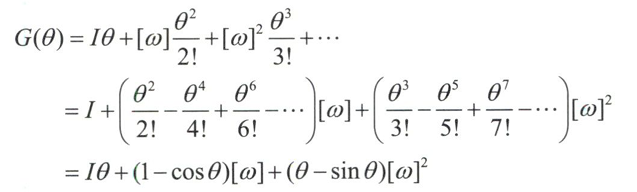
矩阵对数

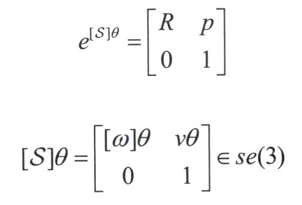
3.4力旋量

将力矩与力合成为—个六维的空间力（spatial lOrce）,称为力旋量（wrench）。

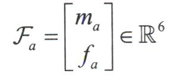
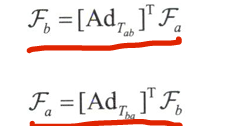
回顾力与速度的点积即为功率，而功率为坐标系无关量，因此有

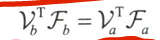
3.5函数

1.计算旋转矩阵的逆
invR = RotInv(R)

2.将三维向量转换为3*3反对称矩阵
so3mat = VecToso3(omg)

3.将3*3反对称矩阵转换为三维向量
omg = so3ToVec(so3mat)

4.从旋转的三维指数坐标中提取出轴线和角度
[omghat,theta] = AxisAng3(expc3)

5.计算矩阵指数对应的旋转矩阵
R = MatrixExp3(so3mat)

6.计算旋转矩阵对应的矩阵对数
so3mat = MatrixLog3(R)

7.M到SO（3）旋转矩阵的空间距离的度量
d = DistanceToSO3(mat)

8.判断M是否为旋转矩阵
judge = TestIfSO3(mat)

9.返回与M最近的旋转矩阵
R = ProjectToSO3(mat)

10.将旋转矩阵和位置向量转换wei
T = RpToTrans(R,p)

11.从变换矩阵中分离出旋转矩阵和位置向量
[R,p] = TransToRp(T)

12.变换矩阵求逆
invT = TransInv(T)

13.构造与六维向量形式的运动旋量V对应的
se3mat = VecTose3(V)

14.构造与se(3)矩阵对应的六维向量形式的运动旋量V
V = se3ToVec(se3mat)

15.计算变换矩阵T的6*6的伴随矩阵
AdT = Adjoint(T)

16.返回正则化的螺旋轴表达式
S = ScrewToAxis(q,s,h)

17.从六位向量形式的指数坐标中提取出螺旋轴和沿轴线移动的距离
[S,theta] = AxisAng6(expc6)

18.计算矩阵指数对应的变换矩阵
T = MatrixExp6(se3mat)

19.计算变换矩阵对应的矩阵对数
se3mat = MatrixLog6(T)

20.M到变换矩阵的空间距离
d = DistanceToSE3(mat)

21.判断是否为SE3变换矩阵
judge = TestIfSE3(mat)

22.离M最近的变换矩阵
T = ProjectToSE3(mat)

（4）正向运动学

4.1指数积公式

现在假定关节$n$对应的关节变量为$\theta$末端坐标系$M$的位移可写成

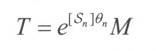
式中，$T \in SO(3)$为末端的新位形’，$S=(\omega_n，v_n)$为表示在基坐标系中的关节$n$的旋量坐标。若关节$n$是转动副（对应的是零节距的螺旋运动），则叫$\omega_n \in R^3$是沿关节轴正向的单位向量，$v_n=-\omega_n\times q_n$，$q_n$为关节轴上任一点，坐标值在基坐标系中进行度量。若关节$n$
是移动副，则叫$\omega_n=0 ，v_n\in R^3$是沿关节轴正向的单位向量，$\theta_n$表示移动的距离。

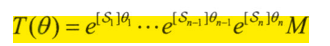
上述方程就是指数积公式的空间坐标表达形式

同样也可以导出物体坐标系的指数积公式

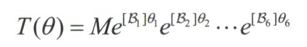
4.2函数

末端坐标系下。给定初始形位，关节旋量以及关节值，计算末端坐标系
T = FKinBody(M,Blist,thetalist)
空间坐标系下。给定初始形位，关节旋量以及关节值，计算末端坐标系
T = FKinSpace(M,Slist,thetalist)

4.3库卡KR60-3运动学建模

import modern_robotics as mr
import numpy as np
from math import pi

omega_1 = np.array([0,0,-1])
omega_2=np.array([0,1,0])
omega_3=np.array([0,1,0])
omega_4=np.array([-1,0,0])
omega_5=np.array([0,1,0])
omega_6=np.array([-1,0,0])

q1=np.array([0,0,0])
q2=np.array([350,0,815])
q3=np.array([1200,0,815])
q4=np.array([2020,0,960])
q5=np.array([2020,0,960])
q6=np.array([2020,0,960])

M=np.array([[ 0,    0,    1,  2190],
            [ 0,    1,    0,     0],
            [-1,    0,    0,   960],
            [ 0,    0,    0,     1]])

# thetalist = np.array([0,-pi/2,pi/2,0,0,0])
thetalist = np.array([-2.410000 / 180 * pi, -57.230000 / 180 * pi, 112.080000 / 180 * pi, -0.780000 / 180 * pi, -54.890000 / 180 * pi,
     1.440000 / 180 * pi])

def vcaculate(omega,q):
    v=np.cross(-omega,q)
    return v
v1=vcaculate(omega_1,q1)
v2=vcaculate(omega_2,q2)
v3=vcaculate(omega_3,q3)
v4=vcaculate(omega_4,q4)
v5=vcaculate(omega_5,q5)
v6=vcaculate(omega_6,q6)

s1=np.append(omega_1,v1)
s2=np.append(omega_2,v2)
s3=np.append(omega_3,v3)
s4=np.append(omega_4,v4)
s5=np.append(omega_5,v5)
s6=np.append(omega_6,v6)

Slist=np.array([s1,s2,s3,s4,s5,s6]).T
# print(M)
# print(v)
# print(thetalist)

T = mr.FKinSpace(M,Slist,thetalist)
print(T)

（5）一阶运动学和静力学

机器人正运动学可以写成
$$
x(t)=f(\theta(t))
$$
对上式关于时间t求导
$$
\dot{x}=\frac {\partial f(\theta) } {\partial \theta }\frac {d(\theta(t)) } {dt }=\frac{\partial f(\theta)} {\partial \theta} = J(\theta)\dot{\theta}
$$

式中，$J(\theta)$被称为雅可比，表示末端执行器速度相对关节速度的线性敏感度，时关于关节变量$\theta$的函数。在某些形位上，雅可比矩阵会变成奇异阵，相应的形位被称为奇异形位，特征主要表现在机器人在末端的某些方向上的速度不能实现。

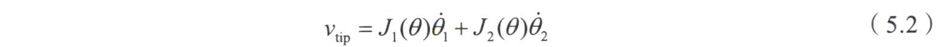
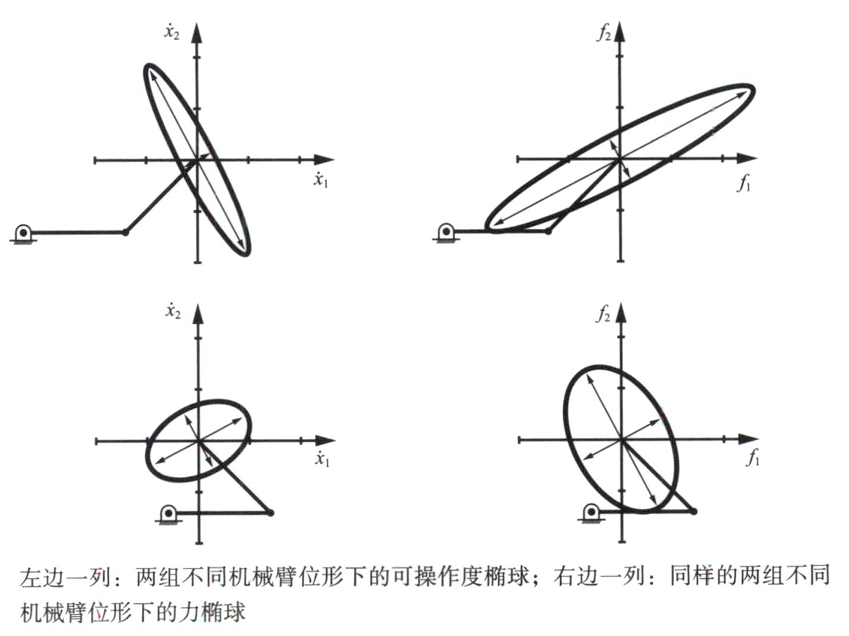
雅可比矩阵可以用来将关节转速的边界映射到$v_{tip}$的边界中，如图5.2所示。不是如图那样将关节速度通过雅可比矩阵映射成多边形，而是在$\dot{\theta}_1-\dot{\theta}_2$平面内将关节速度映射成—个单位圆。这个圆表示关节速度空间的等廓线，其中驱动器的共同作用可考虑为关节速度的平方和。通过映射，单位圆映射成末端速度的—个椭球，这个椭球称为可操作度椭球。当操作手的位形接近奇异位形时，椭球将退化成一个线段，末端沿某方向运动的能力将会丧失。

假设用于机器人运动的功忽略不计，机器人末端施加的功应与关节处产生的功相等，末端力向量记作$f_{tip}$关节力矩向量记作$\tau$
根据能量守恒定律可得

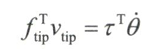
由于$v_{tip}=J(\theta)\dot{\theta}$，因此等式改写为

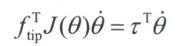
用于生成末端力$f_{tip}$的关节力矩$\tau$可以通过上式计算得到。如果机器人处于非奇异形位，雅可比矩阵及其转置矩阵可逆，可以写成

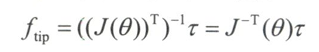
同样，类似于可操作度椭球，可以通过雅可比矩阵的逆转置，将$\tau{1}-\tau{2}$平面内的一个等廓单位圆映射成$f{1}-f{2}$末端力平面的一个椭球，这个椭球被称为力椭球。表示生成不同方向力的难易程度。

由可操作度椭球和力椭球明显可以看出，若在某—方向上比较容易地产生末端速度，该方向产生力就变得比较困难，反之亦然，具体如图5.6所示。事实上，对于给定的机器人位形，可操作度椭球与力椭球的主轴方问完全重合，但力椭球的主轴长度与可操作度椭球的主轴长度正好相反

5.1机器人雅可比

5.1.1空间雅可比

考虑一个n杆的开链机器人，其正向运动学的指数积公式为

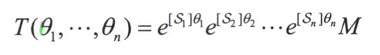
空间速度$V_S$可以写成$[V_S]=\dot{T}T^{-1}$，其中

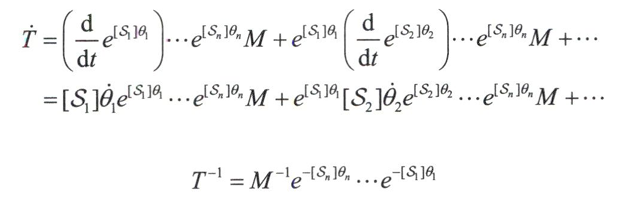
可计算得

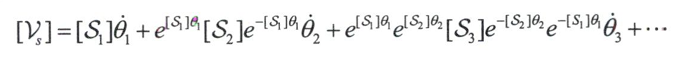
可通过伴随映射写成向量形式

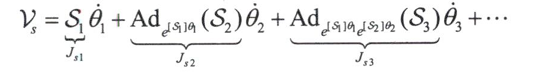
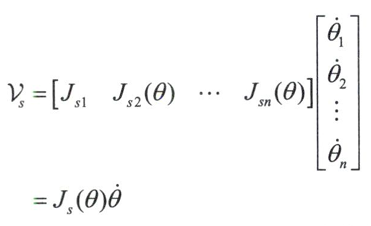
矩阵$J_S(\theta)$即为空间固定坐标形式下得雅可比矩阵，简称为空间雅可比。

$J_{si}(\theta)$得第i列为

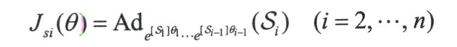
第$i$列的结构形式为$J{si}(\theta)=Ad{T{i-1}}(S{i})$其中$T_{i-1}=e^{[S_1\theta1]}\cdots e^{[S{i-1}\theta_{i-1}]}$。回顾$Si$为机器人处于零位时第i个关节相对固定坐标系的旋量坐标，因此$Ad{T{i-1}}(S{i})$为该机器人经历刚体位移$T_{i-1}$之后的第i个关节相对固定坐标系的旋量坐标。物理上，这与前面的i-l个关节从零位到当前值theta1...thetai-1时的旋量坐标是等效的。因此,$J{s}(\theta)$的第i列$J_{si}(\theta)$只是描述第i个关节轴相对固定坐标系的旋量，同时也是关节变量theta1...theta_i-1的函数。不过是取任意的$\theta$值而不是$\theta$＝0。

5.1.2物体雅可比

物体坐标系下，$[V_b]=T^{-1}\dot{T}$，正运动学公式为

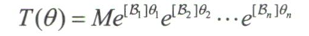
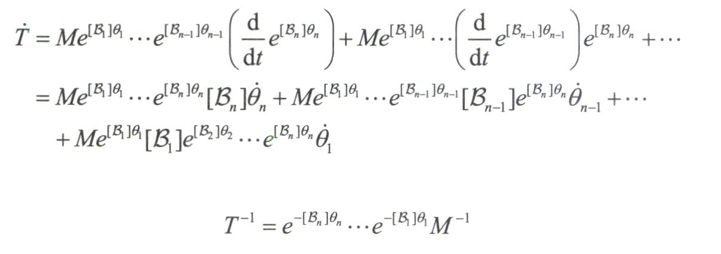
由此计算可得

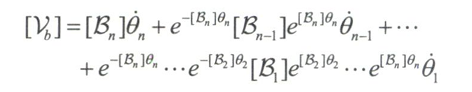
以矩阵形式表示

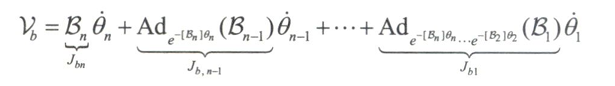
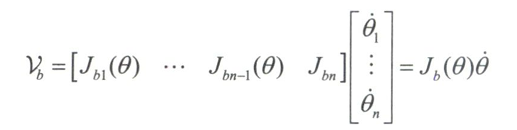
矩阵$J_{b}(\theta)$即为物体坐标系下得雅可比行列式，简称物体雅可比

5.1.3几何解释

5.1.4空间雅可比和物体雅可比的关系

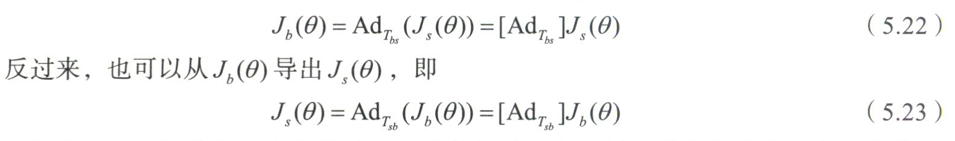
5.1.5几何雅可比和解析雅可比的关系

5.2开链机器人静力学

5.3奇异性分析

​ 如在某个或者多个方向同时失去运动能力的位姿，我们称之为运动学奇异（kinematicsingularjty），或者简称为奇
异（singularity）。数学上,奇异位姿意味着雅可比矩阵$J(\theta)$不再满秩 。

​ 当$J(\theta)$的阶数降到最大值以下，奇异位姿对应此时的$\theta$。奇异位姿下末端坐标系丧失掉在某—维或多维方向的瞬时空间速度，这种奇异下损失的自由度同时伴随产生了与之对应方向上的约束力旋量 。

• 2个旋转轴共轴
• 3各平面转动副轴线平行
• 4各转动副轴线共点
• 4个转动副轴线共面
• 6个转动副都与一条线相交

5.4 可操作度

对于一个通用的″关节开链机器人，任务空间的坐标为q，可操作度椭球对应的是当关节速率满足$|\dot{\theta}|=1$时末端执行器的速度。在n维关节速度空间内的一个单元球。假设$J$可逆,单位关节速度条件数可以写成

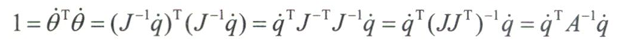
由线性代数可知，上式定义m维空间椭球。椭球主轴方向为$v_i$，主轴半径长为$\sqrt{\lambda_i}$。椭球的体积V与主轴半径长的乘积成正比。

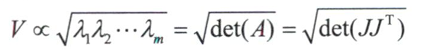
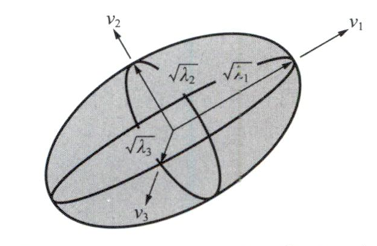
角速度与线速度的量纲不同，于是将雅可比矩阵分开。由此可以得到两个三维可操作度椭球:一个表示角速度,另—个表示线速度。这两个可操作度椭球都有与A的特征向量相对应的主轴，长度为其特征值的平方根。其中，对于角速度可操作度椭球$J=J\omega J\omega^T$，对于线速度可操作度椭球,$J=J_v J_v^T$

当在计算线速度可操作度椭球时’使用物体雅可比$J_b$更合适些,因为我们通常对末端坐标系原点的速度更感兴趣而非固定坐标系原点的速度。

除了可操作度椭球的几何特征之外,还有一种方法是定义可操作度椭球的最长轴半径与最短轴半径的比值

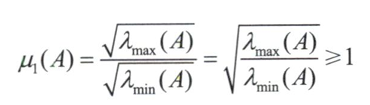
当$\mu_1(A)$接近1时,可操作度椭球接近球形或者各向同性。意味着该机器人沿任何方向都同样容易，这是理想情况。相反,当机器人接近奇异时$\mu_1(A)$趋于无穷大 。

类似的，可以定义$\mu_2(A)$为$\mu_1(A)$的平方，又称为矩阵A的条件数 ，该值越小越理想。矩阵的条件数普遍用于衡量矩阵与向量相乘后的敏感度误差减少的程度 。

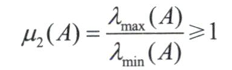
最后一种度量方法是简单利用可操作度椭球的体积，这种情况是越大越好。

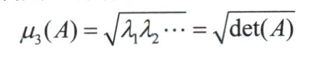
与可操作度椭球类似，可以定义力椭球。 由单位关节力矩满足$||{\tau} ||=1$，得到与上述类似的结果

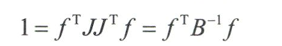
因此，力椭球的主轴长度为可操作椭球长度的倒数。

5.5软件函数

给定物体坐标系下描述的各关节旋量$B_i$及关节角，计算物体雅可比$J_B(\theta)$

Jb=JacobianBody(Blist,thetalist)

给定物体坐标系下描述的各关节旋量$ S_i$及关节角，计算物体雅可比$J_S(\theta)$

J=JacobianBody(Slist,thetalist)

2.改进D-H建模

（1）D-H参数

机器人工具箱中中定义改进DH连杆时一定要注意DH[theta d a alpha]中前两个参数下表为i，即当前关节的DH值，后两个参数下表为i-1，及前一个关节的DH值参数值！

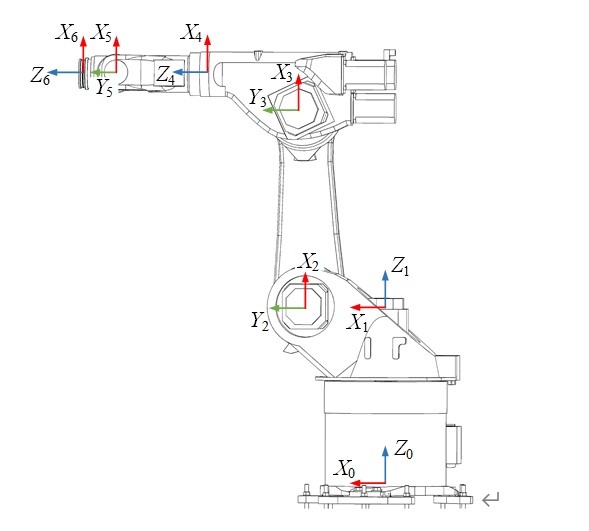
此时对比代码中的DH参数和图中画的坐标系，得到DH定义为

theta(i)：绕Zi轴，从Xi-1旋转到Xi的角度

d(i)：沿Zi轴，从Xi-1移动到Xi的距离

a(i)：沿Xi轴，从Zi移动到Zi+1的距离

alpha(i)：绕Xi轴，从Zi旋转到Zi+1的角度

杆件	theta	d	a	alpha
0	0	0	0	0
1	0	815	350	-90
2	-90	0	850	0
3	0	0	145	-90
4	0	820	0	90
5	0	0	0	-90
6	180	180	0	0

所以在程序中定义DH参数：

杆件	theta	d	a	alpha
1	0	815	0	0
2	-90	0	350	-90
3	0	0	850	0
4	0	820	145	-90
5	0	0	0	90
6	180	180	0	-90

上图所示为机器人处于位姿原点位置，在D-H模型中关节转角theta为[0,-90,0,0,0,180]，而实际的机器人处于原点位姿的关节转角theta'为[0,-90,90,0,0,0]，这是由于机器人关节零位和旋转方向定义与D-H模型不同造成的，实际机器人与D-H模型第一，四，六轴的旋转方向相反，第三、六轴分别差-90°和180°，需要对理论模型和实际模型的关节转角转换关系进行明确的定义：

theta1=-theta1';

theta2=-theta2';

theta3=theta3'-90;

theta4=-theta4';

theta5=-theta5'

theta6=180-theta6'

（2）建模程序

使用python中的机器人工具箱进行D-H建模,程序命名为KR60.py

import roboticstoolbox as rtb
from spatialmath import SE3
from roboticstoolbox import DHRobot, RevoluteDH, RevoluteMDH
from math import pi
import numpy
from numpy import *
import numpy as np

class KR60(DHRobot):
    def __init__(self):
        deg = pi / 180

        # Updated values form ARTE git. Old values left as comments

        L1 = RevoluteMDH(a=0,
                         d=0.815,
                         alpha=0,  # alpha=pi / 2,
                         # theta=0,
                         qlim=[-185 * deg, 185 * deg]
                        )
        L2 = RevoluteMDH(a=0.35,
                         d=0,  # d=0.135,
                         alpha=-pi/2,  # alpha=pi,
                         # theta=0,
                         qlim=[-135 * deg, 35 * deg]
                        )
        L3 = RevoluteMDH(a=0.85,
                        d=0,  # d=0.135,
                        alpha=0,  # alpha=-pi / 2,
                        # theta=-pi/2,
                        qlim=[-120 * deg, 158 * deg]
                        )
        L4 = RevoluteMDH(a=0.145,
                        d=0.82,  # d=0.62,
                        alpha=-pi/2,  # alpha=pi / 2,
                        # theta=0,
                        qlim=[-350 * deg, 350 * deg]
                        )
        L5 = RevoluteMDH(a=0.0,
                        d=0.0,
                        alpha=pi/2,  # alpha=-pi / 2,
                        # theta=0,
                        qlim=[-119 * deg, 119 * deg]
                        )
        L6 = RevoluteMDH(a=0,
                        d=0.17,
                        alpha=-pi/2,
                        # theta=-pi,
                        qlim=[-350 * deg, 350 * deg]
                        )

        L = [L1, L2, L3, L4, L5, L6]

        # Create SerialLink object
        super().__init__(
            L,
            # meshdir="KUKA/KR5_arc",
            name='KR60',
            manufacturer='KUKA')
            # meshdir="meshes/KUKA/KR60_arc")

        self.addconfiguration("qz", [0, -pi/2, 0, 0, 0, pi])
        self.addconfiguration(
          "qk1", [0, -pi/2, 0, 0, 0, 0])
        self.addconfiguration(
          "qk2", [pi / 4, pi / 3, pi / 6, pi / 3, pi / 4, pi / 6])
        self.addconfiguration(
          "qk3", [pi / 6, pi / 3, pi / 6, pi / 3, pi / 6, pi / 3])

if __name__ == '__main__':   # pragma nocover
    robot = KR60()
    print(robot)

在主程序中调用建模程序，同时对实际角度进行相应的转换，转换为D-H模型中对应的关节角进行运算。

import roboticstoolbox as rtb
from spatialmath import SE3
from spatialmath.base import *
import KR60
from math import pi
import math
import numpy
from numpy import *
import numpy as np

def thetaTrans(q):
    q[0] = -q[0]
    q[1] = q[1]
    q[2] = q[2] - pi / 2
    q[3] = -q[3]
    q[4] = q[4]
    q[5] = pi - q[5]
    return q

q = [-2.410000 / 180 * pi, -57.230000 / 180 * pi, 112.080000 / 180 * pi, -0.780000 / 180 * pi, -54.890000 / 180 * pi,
     1.440000 / 180 * pi]
q = thetaTrans(q)
print(q)

robot = KR60.KR60()
T = robot.fkine(q)  
print(T)
T.printline()

得到的结果为

[0.04206243497306334, -0.9988519309163547, 0.38536869884034797, 0.01361356816555577, -0.9580112264196875, 3.1164599123610746]
   0.001189 -0.03091   0.9995    1.569     
  -0.01727   0.9994    0.03092   0.06416   
  -0.9999   -0.01729   0.0006545  0.9428    
   0         0         0         1         

t = 1.57, 0.0642, 0.943; rpy/zyx = -87.8°, 89°, -86.1°

（3） spatialmath-python库

1.函数说明

spatialmath-python库提供了旋转角度，旋转矩阵，四元素，变换矩阵之间的转换函数。

例如，我们可以创建一个刚体变换，它是围绕 x 轴旋转 30 度：

>>> from spatialmath.base import *
>>> rotx(30, 'deg')
array([[ 1.   ,  0.   ,  0.   ],
       [ 0.   ,  0.866, -0.5  ],
       [ 0.   ,  0.5  ,  0.866]])

这将导致一个 NumPy（4x4）数组，该数组属于组（SE3）。我们还可以创建一个类实例：

>>> from spatialmath import *
>>> T = SE3.Rx(30, 'deg')
>>> type(T)
<class 'spatialmath.pose3d.SE3'>
>>> print(T)
   1         0         0         0         
   0         0.866    -0.5       0         
   0         0.5       0.866     0         
   0         0         0         1  

它在内部表示为4*4 NumPy 数组。

虽然函数和类可以提供类似的功能，但该类具有以下优点：

• 类型安全，不可能将3D旋转矩阵与2D刚体运动混合，即使两者都由3*3矩阵表示
• 运算符重载允许方便和可读的算法表达
• 表示的不仅仅是单个值，而是一系列值，这些值由运算符通过隐式广播值进行处理

2.Spatial math 类

如上述所表示的SO3类R,可以计算出相应的欧拉角

>> R.eul()

在机器人技术中，我们经常需要一个序列，一个轨迹，旋转矩阵或姿势。这些姿势类从类继承功能list

>>> R = SO3()   # the identity
>>> R.append(R1)
>>> R.append(R2)
>>> len(R)
 3
>>> R[1]
   1         0         0          
   0         0.955336 -0.29552    
   0         0.29552   0.955336             

这可以在循环和列表理解中使用for

构造它的另一种方法是（在上面定义的R1 R2）

>>> R = SO3( [ SO3(), R1, R2 ] )       
>>> len(R)
 3

许多构造函数支持矢量化，例如 .Rx, .Ry and .Rz

>>> R = SO3.Rx( np.arange(0, 2*np.pi, 0.2))
>>> len(R)
 32

它在一行中创建了旋转矩阵列表。

矢量化也适用于运算符，例如

>>> A = R * SO3.Ry(0.5)
>>> len(R)
 32

将产生一个结果，其中每个元素都是左侧与右侧的每个元素的乘积，即。 R[i] * SO3.Ry(0.5).

同样地

>>> A = SO3.Ry(0.5) * R 
>>> len(R)
 32

将产生一个结果，其中每个元素都是左侧的乘积，即右侧的每个元素。.SO3.Ry(0.5) * R[i]

最后

>>> A = R * R 
>>> len(R)
 32

将产生一个结果，其中每个元素是左侧每个元素与右侧每个元素的乘积，即。.R[i] * R[i]

这些类的基础表示是一个 numpy 矩阵，但该类确保该矩阵的结构对于所表示的特定类有效：SO（2）、SE（2）、SO（3）、SE（3）。任何对类无效的操作都将返回矩阵而不是 pose 类，例如

>>> SO3.Rx(0.3) * 2
array([[ 2.        ,  0.        ,  0.        ],
       [ 0.        ,  1.91067298, -0.59104041],
       [ 0.        ,  0.59104041,  1.91067298]])

>>> SO3.Rx(0.3) - 1
array([[ 0.        , -1.        , -1.        ],
       [-1.        , -0.04466351, -1.29552021],
       [-1.        , -0.70447979, -0.04466351]])

我们也可以打印和打印这些对象

>>> T = SE3(1,2,3) * SE3.Rx(30, 'deg')
>>> T.print()
   1         0         0         1          
   0         0.866025 -0.5       2          
   0         0.5       0.866025  3          
   0         0         0         1          

>>> T.printline()
t =        1,        2,        3; rpy/zyx =       30,        0,        0 deg

>>> T.plot()

二、VREP与PYTHON

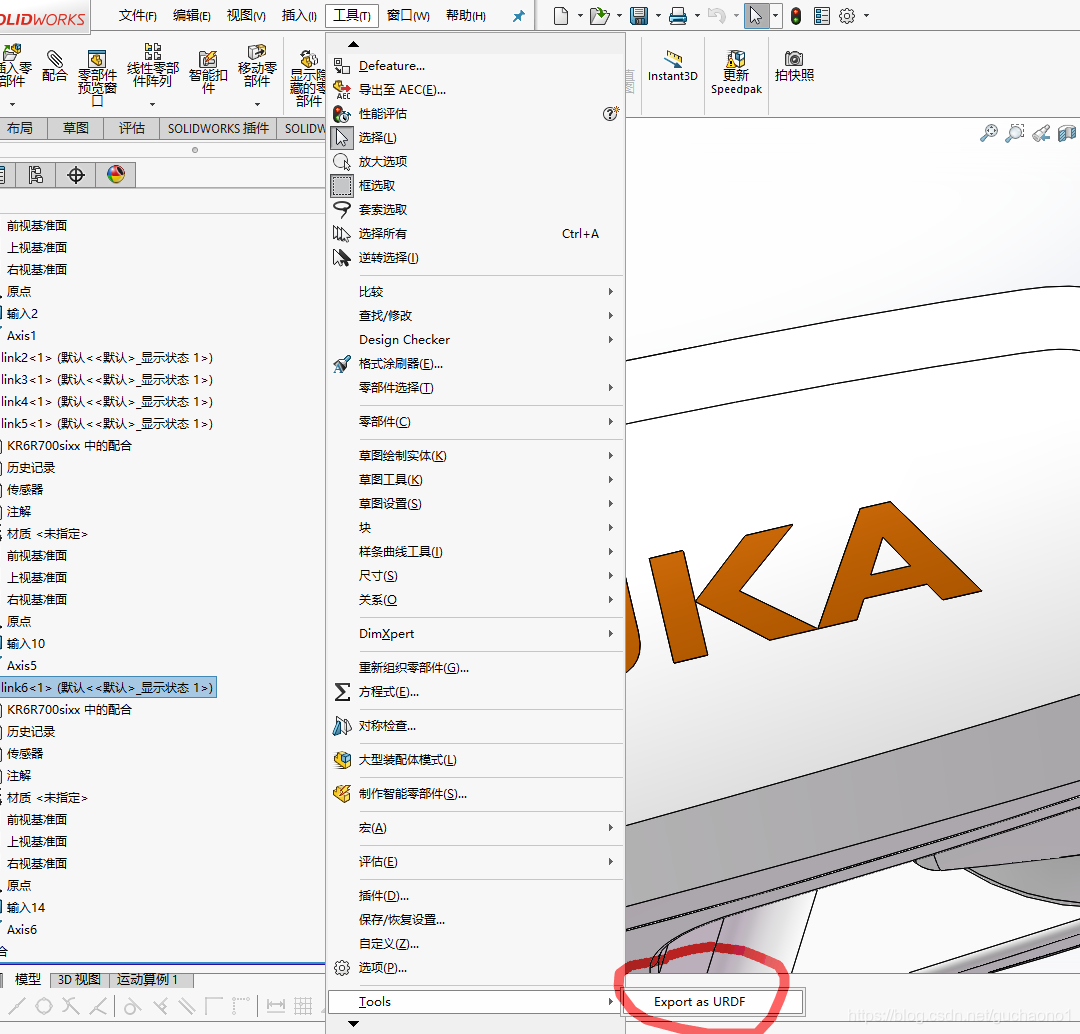
1.建立URDF模型

准备工作：下载solidworks导出urdf文件的插件：http://wiki.ros.org/sw_urdf_exporter ，下载直接安装即可。

1. 去库卡官网下载KR60-3的STL模型

2. 按照面重合-轴线重合的方式，装配好机器人模型。

3. 在装配体中编辑零件，提取关节基准轴，以第六轴为例，命名为axis_6

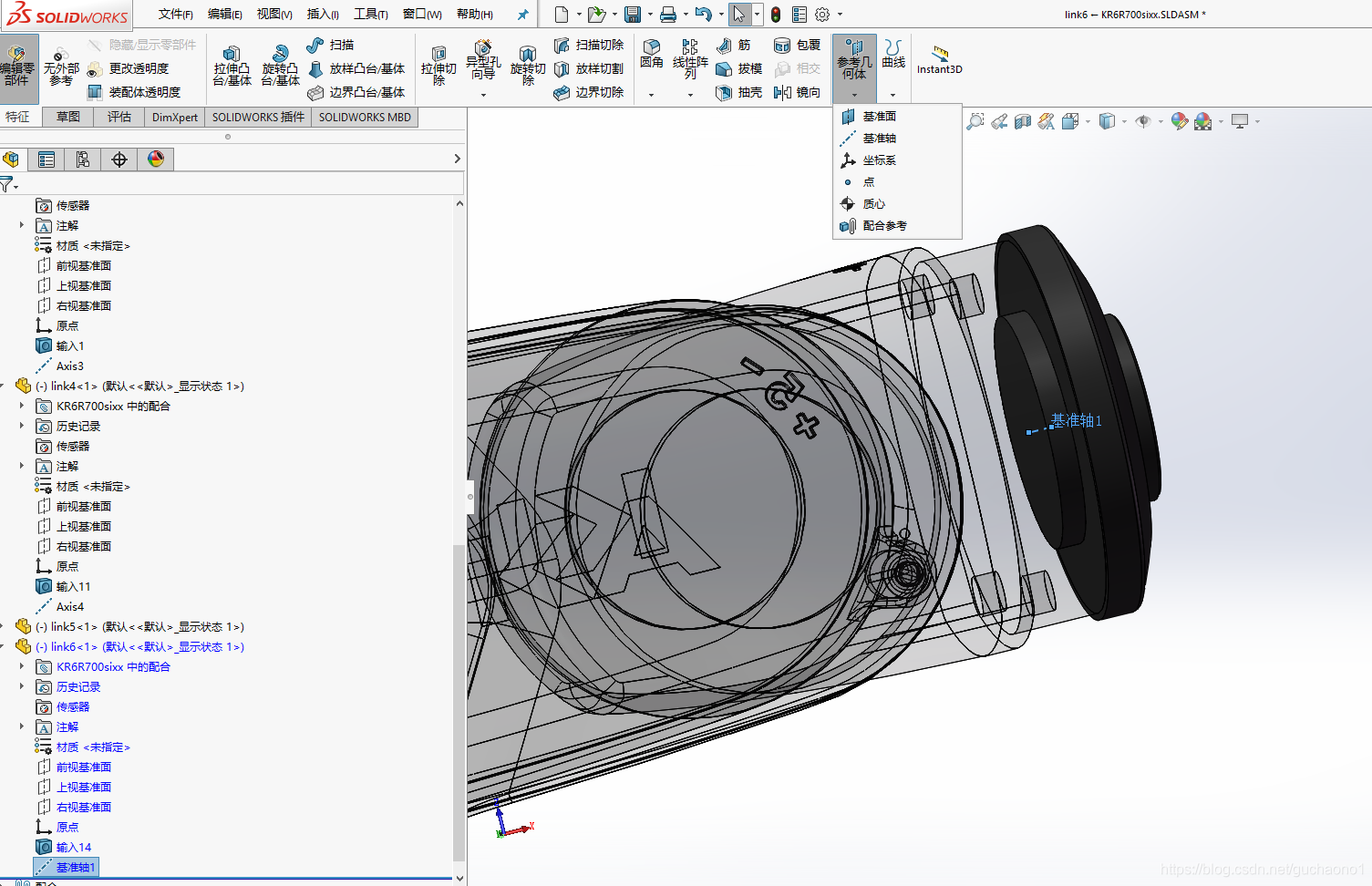
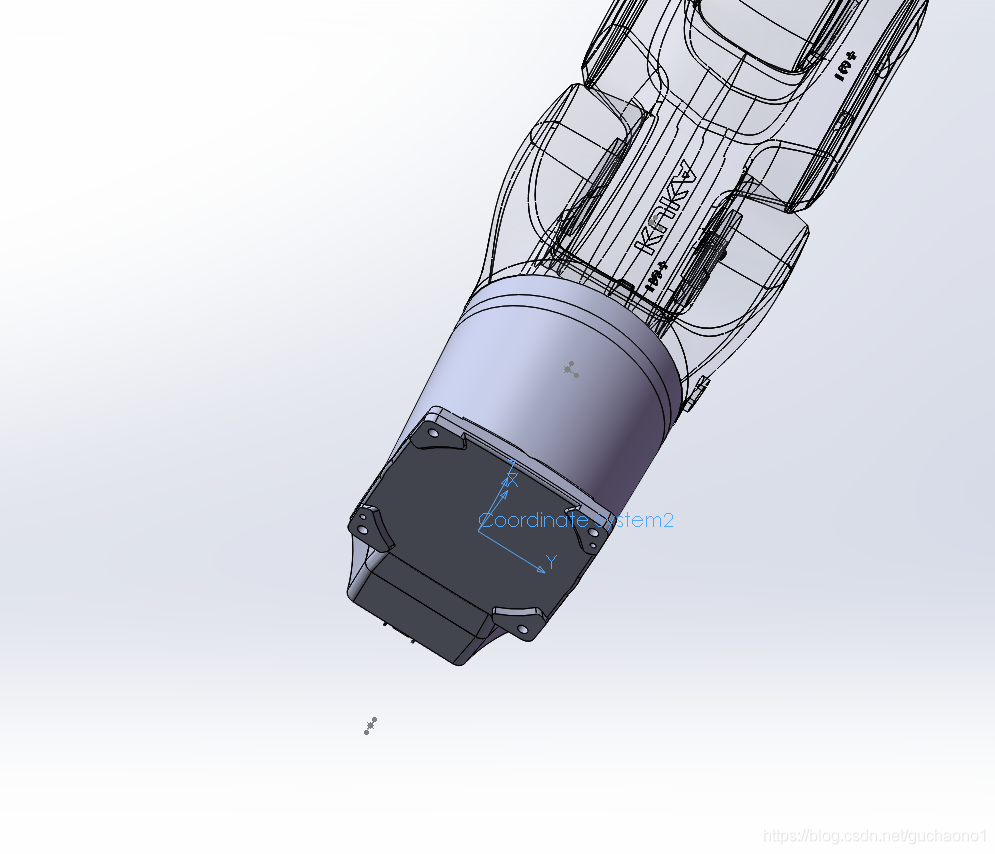
4. 对各关节建立起相应的轴线之后，退出零件编辑，返回装配体设置，对基座、关节以及刀具建立坐标系，注意所建立的坐标系不能在零件的内部，必须在装配体的树形目录下，坐标系的Z轴指向关节旋转方向。

5. 点击工具-tool-export as URDF,轴和坐标系之前建立的关节轴线和坐标轴，零件选择相应的杆件，轴的类型都选择旋转副。

6. 
   导出URDF文件，在最后的配置文件中可以调整杆件的颜色

2.导入VREP

1. 在Vrep中，Plugins-URDF export导入模型文件，注意导入路径不能有中文，否则导入会失败。

2. 将基座设置为固定，调整相应的杆件关节极限,运动模式修改为Torque/force mode。进一步修改杆件的动力学信息，使能电动机，将电动机的最大力矩调整为合适的大小，打开control position enable，修改关节速度极限，这样就可以在脚本中修改关节数据，使机器人按我们设定的轨迹运动。

3. 添加运动脚本，ADD-Associated child scripts-no thread scripts。

   API解释见：regular API reference (coppeliarobotics.com)

   Lua脚本分为4部分，包含由系统适当调用的回调函数集合。除了初始化回调之外，所有其他回调都是可选的。默认主脚本通常分为4个回调函数：

   初始化函数：sysCall_init（）。此回调函数不是可选的。它将在模拟开始时执行一次。代码负责准备模拟等。通过sim.getObjectHandle函数初始化各关节的句柄

   驱动函数：sysCall_actuation()。此回调函数将在每次模拟过程中执行。代码负责处理模拟的所有驱动功能。有一个函数特别有趣：sim.HandleChildScript，它调用子脚本的系统调用回调函数。如果没有这些命令，子脚本将无法执行或无法执行其驱动功能，特定的模型功能或行为也无法按预期运行。

   传感函数：sysCall_sensing()。此回调函数将在每次模拟过程中执行。代码负责以通用方式处理模拟的所有传感功能（接近传感器等）。同样也有sim.HandleChildScript，它调用子脚本的系统调用回调函数。

   恢复函数：sysCall_cleanup()。此函数将在模拟结束前执行一次。该代码负责恢复对象的初始配置、清除传感器状态等。

   function sysCall_init()
      -- do some initialization here
      axis_1_handle = sim.getObjectHandle('axis_1')
      axis_2_handle = sim.getObjectHandle('axis_2')
      axis_3_handle = sim.getObjectHandle('axis_3')
      axis_4_handle = sim.getObjectHandle('axis_4')
      axis_5_handle = sim.getObjectHandle('axis_5')
      axis_6_handle = sim.getObjectHandle('axis_6')
      t = 0
   
      --graph
      graph=sim.getObjectHandle('Graph')
      JointPos=sim.getObjectHandle('JointPos')
   
      objectPosX=sim.addGraphStream(graph,'object pos x','m',1)
      objectPosY=sim.addGraphStream(graph,'object pos y','m',1)
      objectPosZ=sim.addGraphStream(graph,'object pos Z','m',1)
   
      objectJoint1=sim.addGraphStream(JointPos,'Joint1','deg/s',0,{1,0,0})
      objectJoint2=sim.addGraphStream(JointPos,'Joint2','deg/s',0,{1,0.5,0})
      objectJoint3=sim.addGraphStream(JointPos,'Joint3','deg/s',0,{1,1,0})
      objectJoint4=sim.addGraphStream(JointPos,'Joint4','deg/s',0,{1,0,0.5})
      objectJoint5=sim.addGraphStream(JointPos,'Joint5','deg/s',0,{1,0,1})
      objectJoint6=sim.addGraphStream(JointPos,'Joint6','deg/s',0,{1,1,1})
   
      objectTime=sim.addGraphStream(JointPos,'Time','m',1)
   
      sim.addGraphCurve(graph,'object pos x/y/z',3,{objectPosX,objectPosY,objectPosZ},{0,0,0},'m by m')
      sim.addGraphCurve(JointPos,'Joint1',2,{objectJoint1,objectTime},{0,0,0},'m by m')
   
      --base frame
      base_frame = sim.getObjectHandle('baseframe')
   end
   
   function sysCall_actuation()
      -- put your actuation code here
   
      t = t + 0.01
      --print(t)
   
      axis_1_angle = sim.getJointPosition(axis_1_handle)
      axis_2_angle = sim.getJointPosition(axis_2_handle)
      axis_3_angle = sim.getJointPosition(axis_3_handle)
      axis_4_angle = sim.getJointPosition(axis_4_handle)
      axis_5_angle = sim.getJointPosition(axis_5_handle)
      axis_6_angle = sim.getJointPosition(axis_6_handle)
   
      axis_1_targetAngle = math.pi / 3 * math.sin(t)
      axis_2_targetAngle = -math.pi/2 * math.sin(t)
      axis_3_targetAngle = math.pi/2 * math.sin(t)
      axis_4_targetAngle = math.pi/4 * math.sin(t)
      axis_5_targetAngle = math.pi/6 * math.sin(t)
      axis_6_targetAngle = math.pi/5 * math.sin(t)
   
      --print(180*sim.getJointPosition(axis_6_handle)/math.pi)
   
      --print(180*sim.getJointPosition(axis_1_handle)/math.pi)
      --print(axis_1_targetAngle)
      sim.setJointTargetPosition(axis_1_handle,axis_1_targetAngle)
      sim.setJointTargetPosition(axis_2_handle,axis_2_targetAngle)
      sim.setJointTargetPosition(axis_3_handle,axis_3_targetAngle)
      sim.setJointTargetPosition(axis_4_handle,axis_4_targetAngle)
      sim.setJointTargetPosition(axis_5_handle,axis_5_targetAngle)
      sim.setJointTargetPosition(axis_6_handle,axis_6_targetAngle)
      --print(axis_1_angle)
      --print(axis_2_angle)
      --print(axis_2_targetAngle)
   
   end
   
   function sysCall_sensing()
      -- put your sensing code here
      local pos=sim.getObjectPosition(graph,-1)
      --print(pos)
   
      sim.setGraphStreamValue(graph,objectPosX,pos[1])
      sim.setGraphStreamValue(graph,objectPosY,pos[2])
      sim.setGraphStreamValue(graph,objectPosZ,pos[3])
   
      sim.setGraphStreamValue(JointPos,objectJoint1,180*sim.getJointPosition(axis_1_handle)/math.pi)
      sim.setGraphStreamValue(JointPos,objectJoint2,180*sim.getJointPosition(axis_2_handle)/math.pi)
      sim.setGraphStreamValue(JointPos,objectJoint3,180*sim.getJointPosition(axis_3_handle)/math.pi)
      sim.setGraphStreamValue(JointPos,objectJoint4,180*sim.getJointPosition(axis_4_handle)/math.pi)
      sim.setGraphStreamValue(JointPos,objectJoint5,180*sim.getJointPosition(axis_5_handle)/math.pi)
      sim.setGraphStreamValue(JointPos,objectJoint6,180*sim.getJointPosition(axis_6_handle)/math.pi)
   
      --Joint1={}
      --table.insert(Joint1,axis_1_angle)
      --sim.setGraphStreamValue(JointPos,objectJoint1,Joint1)
   end
   
   function sysCall_cleanup()
      -- do some clean-up here
   end
   
   -- See the user manual or the available code snippets for additional callback functions and details
   

   4. 点击仿真进行按钮，机器人就按着脚本中关节设置的轨迹进行移动，同时在空间中绘制出末端的运行轨迹，在弹出的框中也可以看到末端在XY平面的轨迹。

3.联合仿真

Vrep提供了三种远程api，远程API是应用程序与CoppeliaSim连接的几种方式之一。它允许CoppeliaSim和外部应用程序（即在不同进程或不同机器上运行的应用程序）之间的通信，是跨平台的，支持服务调用（即阻塞调用），还支持双向数据流。它有三种不同的版本/框架：

The ZeroMQ-based remote API：它轻量级且易于使用，提供了通过CoppeliaSim脚本也可用的所有API函数，目前支持Python客户端。

The legacy remote API (or simply remote API)：它相对轻量级，并且比基于B0的远程API具有更少的依赖性。它提供了API函数的子集，并支持以下客户端：C/C++、Java、Python、Matlab、Octave和Lua。

The B0-based remote API：它基于BlueZero中间件及其与CoppeliaSim的接口插件。它提供了API函数的子集，可以很容易地扩展和支持以下客户端：C++、java、python、Matlab和Lua。

1.Vrep与matlab联合仿真

Legacy remote API

要在Matlab程序中使用远程API功能，需要以下3项：

• remoteApiProto.m

• remApi.m

• remoteApi.dll

  • 新建一个matlab项目文件夹

  • 将C:\Program Files\CoppeliaRobotics\CoppeliaSimEdu\programming\remoteApiBindings\matlab\matlab中所有的文件拷贝到相应的matlab项目文件夹中。

  • 转到C:\Program Files\CoppeliaRobotics\CoppeliaSimEdu文件夹，调整类型只显示应用程序拓展，全选所有的DLL文件，拷贝到matlab文件夹。

  • remoteapi.dll在C:\Program Files\CoppeliaRobotics\CoppeliaSimEdu\programming\remoteApiBindings\lib\lib\Windows文件夹中，同样拷贝到项目文件夹

  • 打开matlab，将项目文件夹包含到预定路径中，使程序在运行中能调用相应的函数和dll文件。

在Matlab的当前文件夹中包含上述文件后，调用sim=remApi（'remoteApi'）来构建对象并加载库。要在客户端（即您的应用程序）启用远程API，请调用sim.simxStart。请参阅simpleTest。以编程/remoteApiBindings/matlab目录中的m程序为例。本页列出并描述所有支持的Matlab远程API函数。CoppeliaSim远程API函数可以很容易地从它们的“simx”前缀中识别出来。
确保您的Matlab使用与remoteApi库相同的位体系结构：64位Matlab和32位remoteApi库将无法工作，反之亦然！

关键的语句

V-REP端：
simExtRemoteApiStart(19999)

MATLAB端：
vrep=remApi('remoteApi'); % using the prototype file (remoteApiProto.m)
vrep.simxFinish(-1); % just in case, close all opened connections
clientID=vrep.simxStart('127.0.0.1',19999,true,true,5000,5);

B0-based remote API

python

1. 要在Python脚本中使用基于B0的远程API功能，您需要以下内容：

• 安装用于Python的MessagePack:pip install msgpack
• C:\Program Files\CoppeliaRobotics\CoppeliaSimEdu\programming\b0RemoteApiBindings\python\b0RemoteApi.py
• C:\Program Files\CoppeliaRobotics\CoppeliaSimEdu\programming\b0RemoteApiBindings\python\b0.py。
• blueZero库（例如b0.dll），不要忘记blueZero库本身有依赖项（例如libzmq, boost_chrono, boost_system, boost_thread等）。

2. 创建anaconda虚拟环境

   1、用conda创建Python虚拟环境（在conda prompt环境下完成）
   conda create -n Vrep python=3.7
   
   2、激活虚拟环境（在conda prompt环境下完成）
   activate Vrep
   
   3、给虚拟环境安装外部包
   conda install -n Vrep [package]
   例如: conda install -n tensorflow pandas
   
   4、查看已有的环境(当前已激活的环境会显示一个星号)
   conda info -e
   
   5、删除一个已有的虚拟环境
   conda remove --name your_env_name --all
   
   6、查看pip的安装目录
   pip list
   
   7、删除已经安装的模块
   pip uninstall **
   (例如：pip uninstall numpy)

   创建anaconda的虚拟环境后，会生成E:\Anaconda\envs\Vrep的文件夹，在Pycharm中选择创建的虚拟环境。

   3. 和matlab操作一样，打开C:\Program Files\CoppeliaRobotics\CoppeliaSimEdu文件夹，调整类型只显示应用程序拓展，全选所有的DLL文件，拷贝到anaconda创建的虚拟环境的文件夹中。b0RemoteApi.py，b0.py拷贝到项目文件夹中，在pycharm控制台中使用，conda install msgpack下载msgpack包

   4. 打开Vrep端的服务器，直接在model browser中打开tools文件夹，将B0 Remote API Server拖动到场景中，就打开了Vrep端的服务器

   5. 打开python端的服务器

import b0RemoteApi
import time

with b0RemoteApi.RemoteApiClient('b0RemoteApi_pythonClient','b0RemoteApi') as client:
    def getJointPos(num):
        jointname = "axis_" + str(num)
        [bool, jointhandle] = client.simxGetObjectHandle(jointname, client.simxServiceCall())
        [bool, joint] = client.simxGetJointPosition(jointhandle, client.simxServiceCall())
        print(joint)
        return joint
    client.simxStartSimulation(client.simxServiceCall()) #开始仿真
    startTime = time.time()
    getJointPos(1)
    while time.time() < startTime + 5:
        continue
    client.simxStopSimulation(client.simxServiceCall()) #停止仿真

基于B0的远程API操作方法

大多数基于B0的远程API函数需要一个附加参数：用于执行函数调用的主题或通信通道。

主题可以是以下5个函数之一的返回值：
simxServiceCall：本主题允许在阻塞模式下执行功能，即命令将传输到服务器（即CoppeLisim），在那里执行，并向客户端返回响应。仅当作为一次性操作从服务器获取命令响应时（例如，simxGetObjectHandle通常使用服务调用来执行）才使用此主题。
simxDefaultPublisher：本主题允许在非阻塞模式下执行函数，即函数被发送到服务器（即CoppeliaSim），控制权立即返回到客户端（即客户端不会等待服务器的回复）。仅在向服务器发送命令时使用此主题，您不希望/不需要服务器响应（例如，simxSetJointPosition通常使用默认发布服务器执行）。
simxDefaultSubscriber：本主题通知服务器持续执行该函数，并持续将响应流式传输到客户端。客户端将在回调函数中接收响应。仅当您希望从服务器端连续执行的同一命令接收响应时，才使用此主题。（例如，simxGetJointForce通常使用默认订阅服务器执行）。定义的回调函数通过simxSpinOnce函数调用（当输入缓冲区中有响应可用时）。
simxCreatePublisher：这与simxDefaultPublisher非常相似，不同之处在于创建了一个专用的发布者主题，即创建了一个专用的发布频道。将特定功能/命令分配给专用发布服务器非常有用，特别是在数据量大的情况下（例如，simxSetVisionSensorImage通常使用专用发布服务器执行）。
simxCreateSubscriber：这与simxDefaultSubscriber非常相似，不同之处在于创建了专用订户主题，即创建了专用订户频道。将特定功能/命令分配给专用订阅者可能很有用，特别是在数据量大的情况下（例如，simxGetVisionSensorImage通常使用专用订阅者来执行）。
默认情况下，基于B0的远程API客户端和服务器（即CoppeliaSim）将异步运行。但是，为了实现同步操作，可以让客户端单独触发每个模拟步骤。以下是同步模式的Python示例：

import b0RemoteApi
import time

with b0RemoteApi.RemoteApiClient('b0RemoteApi_pythonClient','b0RemoteApi') as client:    
    doNextStep=True

    def simulationStepStarted(msg):
        simTime=msg[1][b'simulationTime'];
        print('Simulation step started. Simulation time: ',simTime)

    def simulationStepDone(msg):
        simTime=msg[1][b'simulationTime'];
        print('Simulation step done. Simulation time: ',simTime);
        global doNextStep
        doNextStep=True

    client.simxSynchronous(True)
    client.simxGetSimulationStepStarted(client.simxDefaultSubscriber(simulationStepStarted));
    client.simxGetSimulationStepDone(client.simxDefaultSubscriber(simulationStepDone));
    client.simxStartSimulation(client.simxDefaultPublisher())

    startTime=time.time()
    while time.time()<startTime+5: 
        if doNextStep:
            doNextStep=False
            client.simxSynchronousTrigger()
        client.simxSpinOnce()
    client.simxStopSimulation(client.simxDefaultPublisher())

三、仿真

四、python小知识

1.创建anaconda虚拟环境

1、用conda创建Python虚拟环境（在conda prompt环境下完成）
conda create -n Vrep python=3.7

2、激活虚拟环境（在conda prompt环境下完成）
activate Vrep

3、给虚拟环境安装外部包
conda install -n Vrep [package]
例如: conda install -n tensorflow pandas

4、查看已有的环境(当前已激活的环境会显示一个星号)
conda info -e

5、删除一个已有的虚拟环境
conda remove --name your_env_name --all

6、查看pip的安装目录
pip list

7、删除已经安装的模块
pip uninstall **
(例如：pip uninstall numpy)

创建anaconda的虚拟环境后，会生成E:\Anaconda\envs\Vrep的文件夹，在Pycharm中选择创建的虚拟环境。

2.pip换镜像源

在 python 里经常要安装各种这样的包，安装各种包时最常用的就是 pip，pip 默认从官网下载文件，官网位于国外，下载速度时快时慢，还经常断线，国内的体验并不太好。

解决办法是把 pip 源换成国内的，最常用的并且可信赖的源包括清华大学源、豆瓣源、阿里源：

pypi 清华大学源：https://pypi.tuna.tsinghua.edu.cn/simple
pypi 豆瓣源 ：http://pypi.douban.com/simple/
pypi 腾讯源：http://mirrors.cloud.tencent.com/pypi/simple
pypi 阿里源：https://mirrors.aliyun.com/pypi

pip 源具体修改方式是，我们以安装 python 的robotics-toolbox-python模块为例，通常的方式是直接在命令行运行

pip install robotics-toolbox-python

这样会从国外官网下载robotics-toolbox-python模块并安装。

若要把 pip 源换成国内的，只需要把上面的代码改成下图这样（下图以清华大学源为例）：

pip install robotics-toolbox-python -i https://pypi.tuna.tsinghua.edu.cn/simple

这样我们就从清华大学源成功安装了机器人工具箱，速度会比过pip默认的国外源快很多。

上述做法是临时改成国内源，如果不想每次用 pip 都加上 -i https://pypi.tuna.tsinghua.edu.cn/simple，那么可以把国内源设为默认，做法是：

# 清华源
pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simple
# 阿里源
pip config set global.index-url https://mirrors.aliyun.com/pypi/simple/
# 腾讯源
pip config set global.index-url http://mirrors.cloud.tencent.com/pypi/simple
# 豆瓣源
pip config set global.index-url http://pypi.douban.com/simple/