对于给定的加工任务,冗余自由度和变位器转角都会对机器人的加工位姿造成影响。因此,可以通过改变变位器的姿态和冗余自由度,进一步利用机器人的灵活性能,提高机器人的铣削加工性能。在上一篇文章中分别分析了冗余度和变位器转角与机器人刚度的关系,并提出了基于刚度的曲面轨迹分割方法。
本文在次基础上,得到分割后的加工轨迹,同时对冗余度和变位器进行优化,考虑机器人的运动学和碰撞约束,获取每个子区域的最优的冗余度和变位器参数,使整个加工区域的整体刚度指标最优。针对传统算法在进行优化时难以收敛的问题,使用强化学习算法DDPG建立模型优化环境,设计轨迹优化的马尔可夫决策过程,通过DDPG算法的不断学习,实现加工轨迹的最优化。
1 、基于整体刚度指标的加工轨迹优化模型
本节以提高机器人加工过程中的刚度指标$H$为目标,建立一个同时考虑变位器和冗余度的轨迹优化模型。对于一个给定的五轴加工任务,机器人的加工姿态$(X,Y,Z,A,B,C)$会随变位器旋转角度和机器人冗余度的变化而变化。由前文刚度模型的推导可知,机器人刚度随姿态变化而变化,在加工任务确定的情况下,机器人姿态由冗余自由度和工件设置决定,所以机器人刚度可以看作是关于冗余度和变位器转角的函数。
$$
f_{st}(\alpha_1,\beta_1,...,\alpha_n,\beta_n)=H(\alpha_1,\beta_1,...,\alpha_n,\beta_n)
$$
根据前文的轨迹分割,假设将加工轨迹分割为$n$个不同的子区域,每个区域对应一组最优冗余角和变位器旋转角,优化目标函数设为机器人在加工任务的整体刚度指标$H$,并且其是冗余角和变位器旋转角的函数,如下所示:
$$
\mu(\theta)=\sqrt{det(J(\theta)J(\theta)^T)}
$$
另外,机器人加工轨迹优化中还需要考虑许多约束条件,首先,机器人姿态应该避免处于奇异形位或者奇异形位附近。
其次,为了避免加工过程中达到机器人关节极限姿态,加工过程中机器人的各个关节角也应该受到限制,机器人的关节角要处于各个关节的转动范围内,同时也要考虑机器人关节速度不超过关节速度极限,即:
$$
\theta{min}\leq \theta \leq \theta{max}
$$
$$
\Delta \theta \leq \Delta \theta {max}
$$
通过可操作度、关节和关节速度等约束,建立起基于分区域轨迹优化方法的变位器旋转角度和机器人冗余角的优化模型。
最后,在对机器人轨迹进行优化后,还需要进一步考虑碰撞问题。在加工平台中,有工件、变位器和夹具等辅助设备,机器人与加工系统发生碰撞不仅会对设备产生损伤,而且会危及研究人员的人身安全,在加工过程中,必须保证机器人不会存在碰撞的发生。因此,使用CoppeliaSim中的物理引擎进行碰撞检测,保证优化后的轨迹在加工过程无碰撞,如图所示。
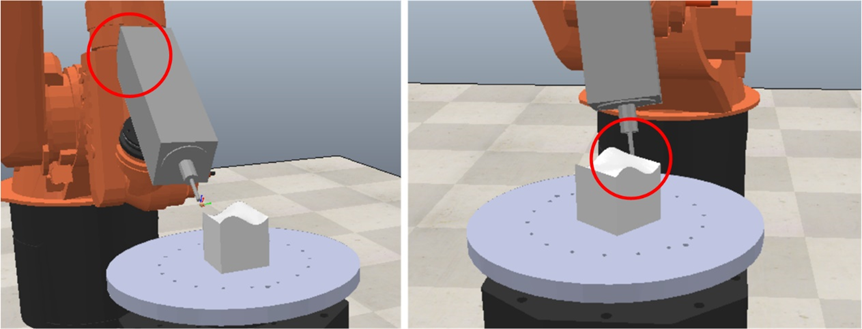
2 、基于强化学习的机器人轨迹优化方法
上一节所展示的是一个多维优化问题,问题复杂度会随着区域划分数量的增长而增长。由前文的刚度分析可知,加工区域的整体刚度不是跟随变位器旋转角和机器人冗余角单调变化的。在求解这种高维问题时,使用启发式算法存在陷入局部最优的问题,本节提出使用深度确定性策略梯度算法 (Deep Deterministic Policy Gradient, DDPG)来对加工轨迹各个子区域的变位器转角和机器人冗余角参数进行优化。
2.1 基于参数优化的马尔可夫决策过程设计
强化学习是一种基于马尔可夫决策过程的人工智能机器学习算法,在机器人研究领域得到广泛应用。本文对机器人曲面加工轨迹优化问题进行了建模,优化目标为最大化机器人加工过程中的整体刚度指标$H$,将问题转换为马尔可夫决策过程,包括状态空间,动作空间和奖励函数的设计。
如图所示,智能体和环境分别是强化学习的主要元素,智能体根据当前状态$s$来产生下一的动作$a$,并产生当前的奖励$r$。当智能体的动作导致了奖励为正值,智能体后续产生这个动作的概率就会上升,若奖励为负值,智能体产生这个动作的概率就会下降,通过迭代不断优化智能体,使智能体在环境中找到最优解。
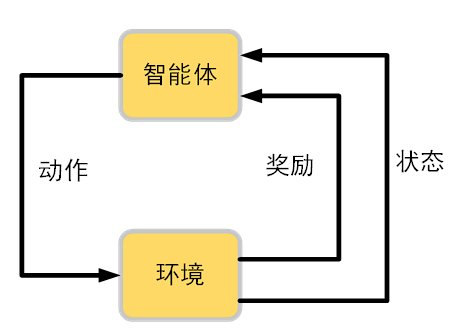
状态空间设计:在机器人加工轨迹参数优化问题中,状态设置为优化模型中变量的信息,即由各个加工区域的冗余自由度$ α_i$和变位器旋转角$β_i$组成的集合 。
动作空间设计:在本文的优化模型中,动作空间根据优化变量的变化而设计,加工参数即各个区域的冗余自由度αi和变位器旋转角βi可以增大、减小或者不变。在DDPG中,参数的变化可以是连续的动作,选择各个参数的动作空间为各个加工参数的变化量 ,根据优化的经验,选择动作空间范围为[-1,1]。
奖励函数构建:奖励函数主要通过参数模型优化目标和优化适应度函数进行构建。奖励用于评价当前状态$s_t$下选取动作$a_t$对环境的好坏影响,奖励函数的设计会影响算法的寻优性能,通常根据寻优目标进行设计,本文的目标是最小化机器人加工的整体刚度指标$H$,$DDPG$算法的目标是使累计奖励最大,因此奖励函数应与整体刚度指标$H$呈负相关。
2.2 DDPG算法原理
DDPG是一种基于策略梯度的强化学习算法。与DQN基于值的强化学习训练方法不同,DDPG通过梯度来更新网络,使其向累计奖励增高的方向进行更新。DDPG算法可以处理连续空间问题,且在高维优化问题上适应性较强,而基于区域分割的机器人参数优化问题是一个高维且连续的问题,因此DDPG算法比较适合本文的参数优化问题。
DDPG算法基于Actor-Critic框架,通过训练以及环境的奖励机制不断更新网络,如图所示。
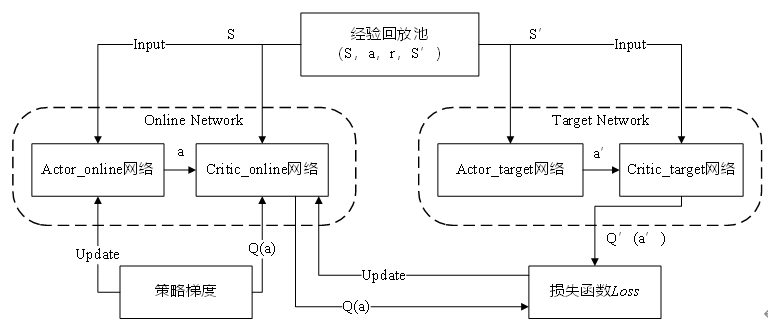
Actor和Critic分别各自含有两个神经网络,因此,DDPG有四个网络,即:Actor_online、Actor_target、Critic_online和Critic_target。其核心思想是用Actor网络输出一个确定的动作,然后使用Critic网络对动作进行评估,最后对Actor网络进行更新。
Actor网络根据状态输出一个确定的动作$a$,Critic_online对动作进行评估,利用策略梯度的方法更新Actor_online:
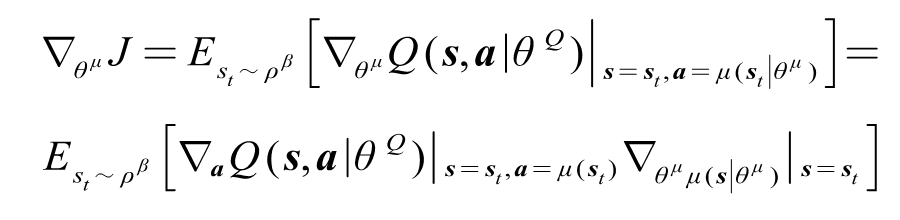
Critic_target网络对动作$a$进行评估,计算Critic网络的损失函数,利用反向传播更新Critic_online:
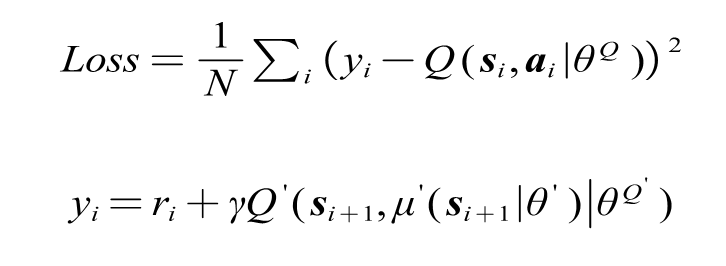
最后,在经过一定次数的训练后,更新Actor_target和Critic_target网络:
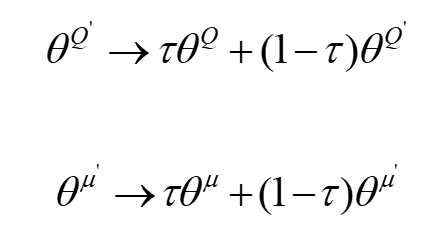
3.3 基于DDPG的参数优化流程
基于DDPG算法,以最大化奖励$r_t$为目标,将优化的参数作为优化变量$ s_t$,通过智能体的不断迭代,得到使累计奖励最高的状态$s_t$,即机器人整体刚度指标$H$最优的加工参数。DDPG的算法步骤可以见表所示:

3 优化结果与分析
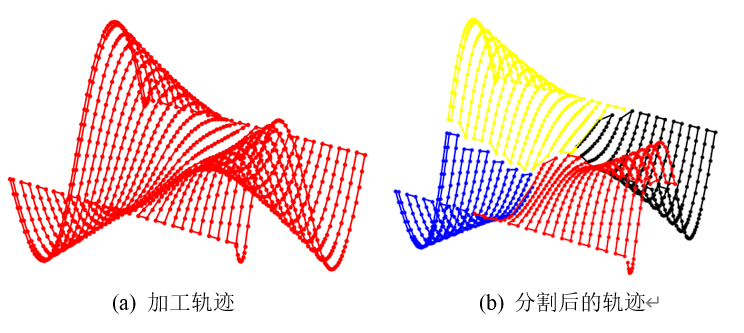
首先,使用DDPG算法与其他常用的启发式优化算法对优化模型进行求解,并对求解效果进行比较,对算法的优化性能在多个方面进行评价,优化轨迹如图所示,为一个凹凸不平的自由曲面,本文使用第3章所示轨迹分割方法,将其分割为4个子区域。
使用Tensorflow框架进行DDPG的设计,在Intel Core i7-7600HQ CPU和GTX965M GPU的硬件配置上运行。关于DDPG算法的参数设置如表所示:

DDPG算法训练结束后,输出最优状态,为了对比DDPG算法与启发式算法之间的优化过程,用于验证DDPG算法进行参数优化的性能。给定一组加工任务,将DDPG算法与粒子群算法(PSO)和遗传算法(GA)等启发式算法进行对比。