机器人铣削运动链

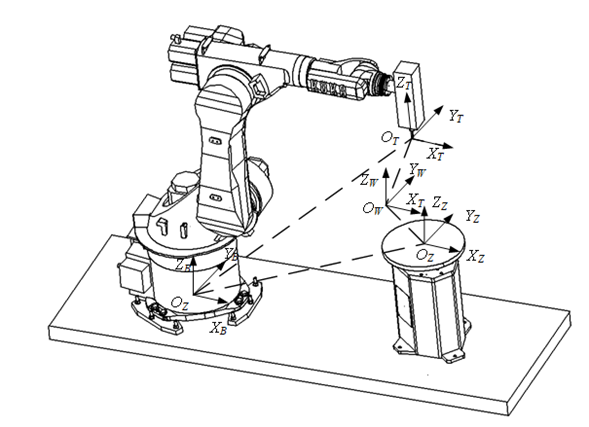
如图所示为机器人铣削系统，由机器人本体、变位器、工件以及电主轴组成，机器人通过底座本体固定于地面，而电主轴通过刚性连接固定于末端法兰。机器人铣削系统包括了多个参考坐标系，机器人基坐标系XB-YB-ZB定义于机器人底座中心，机器人工具坐标系XT-YT-ZT可通过电主轴标定确定，变位器坐标系XZ-YZ-ZZ定义在变位器的中心位置，会根据变位器的旋转运动而发生变化，工件坐标系XW-YW-ZW会根据工件的装夹位置和姿态进行确定，要对机器人铣削系统进行运动链分析，需要对各个坐标系进行标定。

工具坐标系标定

机器人末端工具坐标系XT-YT-ZT的标定分为电主轴刀尖原点和姿态的确定。电主轴刀尖原点可以使用XYZ 4点法和XYZ参照法进行测量，电主轴刀尖姿态可以使用ABC世界坐标法和ABC两点法进行测量。

工件坐标系标定

要实现工件坐标系XW-YW-ZW的标定，需要对工件变位器坐标系XZ-YZ-ZZ进行标定。首先，在变位器上确定一个参照点，并在机器人系统中输入其距离变位器中心的距离。将已标定的工具坐标系移动至参考点，并对工具坐标系位置进行测量保存，重复上述步骤3次，每次重复前都需要转动变位器，以便工具坐标系从不同的出发位置移动到参考点，如图所示。

使用已标定好的电主轴确定工件坐标系的原点，机器人控制系统会计算工件坐标系原点与变位器坐标系之间的相对位置，通过ABC 2点法确定工件坐标系相对于变位器的姿态，得到了工件坐标系相对于变位器的相对位姿。

在完成工件坐标系的标定后，还需要确定变位器的运行模式，变位器有两种运行模式，一种是同步运行模式，通过在KUKA KRL程序中将机器人基坐标系与变位器相关联，这样机器人与变位器会同步运行；另一种是非同步模式，在KUKA KRL程序中将变位器与基坐标系解除关联，机器人与变位器会按一定顺序先后运行。为了提高机器人加工系统的稳定性，铣削加工中通常使用非同步模式。

运动链分析

如图2-5所示为机器人铣削系统，机器人铣削系统中各个坐标系形成一个闭环，构成了一个完整的运动链，机器人末端坐标系XT-YT-ZT的姿态在基坐标系中可以定义为：
$$
_{tool}^BT={Z^B}T\cdot T{roz}(\beta)\cdot{W^Z}T\cdot {{tool}^W}T
$$
其中，$Z^B{T}$为基坐标系下变位器的位姿矩阵，$T{roz}(\beta)$为变位器绕自身Z轴旋转β后的变换矩阵，$W^Z{T}$为工件坐标系相对于变位器的位姿矩阵，与工件装夹位置有关，${tool}^W{T}$为给定的加工任务。

UG软件生成的加工轨迹通常适用于数控加工，轨迹信息包括加工位置$\boldsymbol{P}_{\mathrm{tool}}^{\mathrm{Z}}$和刀轴方向矢量V\tool。要确定机器人末端工具的加工轨迹，需要将五轴加工任务转换为机器人末端的六自由度运动轨迹，即机器人末端的位置(X,Y,Z)和姿态(A,B,C)。与机器人运动轨迹相比，五轴加工的位置和刀轴方向是确定的，但缺少一个绕刀轴旋转方向的冗余自由度α，如图2-11所示。