一、冗余自由度

刀具路径由离散的CLS数据组成，
$$
CLS=(x,y,z,i,j,k)
$$
其中x,y,z为刀具位置，i,j,k为刀轴方向的单位向量

1、CLS对应的末端姿态

方法一：

引用文献中的方法

Peng J, Ding Y, Zhang G, 等. Smoothness-oriented path optimization for robotic milling processes[J]. Science China Technological Sciences, 2020, 63(9): 1751–1763.

由cls可以生成刀具姿态，但是刀具姿态并不唯一，定义初始机器人任务姿态为：

$o_i=(x,y,z)$为刀具姿态矩阵的位置，z轴向量为
$$
z_i = （i，j，k）
$$
x轴向量为
$$
x_i=y_i \times z_i
$$
y轴向量可以有下式计算得来
$$
y_i= \frac{zi \times \overline{o{i+1} o_{i}} } {\lVert {zi \times \overline{o{i+1} o_{i}}} \lVert}\
对于最后一个cls点\
y_i= \frac{zi \times \overline{o{i-1} o_{i}} } {\lVert {zi \times \overline{o{i-1} o_{i}}} \lVert}\
$$
由此可以得到机器人末端初始姿态矩阵，因为绕刀具轴的旋转对铣刀定位没有影响，因此对于一个CLS，存在无数的可行机器人姿态，可由绕刀轴旋转得到。
$$
T(\gamma_i) = T_i \cdot Rot(\hat{z},\gamma_i)\
T_i = \begin{bmatrix}
x_i&y_i&z_i&o_i\
0&0&0&1\end {bmatrix}\
$$
其中$T_i$为cls对应的初始末端矩阵，$\gamma \in [-\pi,\pi]$为冗余自由度，这样就可以得到CLS任意冗余自由度对应的末端姿态矩阵。

这种方法会导致刀具轨迹弯折时机器人姿态变化较大

方法二：

[1]Zhu W, Qu W, Cao L, 等. An off-line programming system for robotic drilling in aerospace manufacturing[J]. The International Journal of Advanced Manufacturing Technology, 2013, 68(9–12): 2535–2545.

定义与上一个的方法一样，$z_i = [i,j,k]$，而$x_i$是三个标准单位向量$[1,0,0],[0,1,0],[0,0,1]$在由$[x,y,z]和[i,j,k]$决定的平面上的最长投影的归一化向量，$y_i$是$z_i$和$x_i$的叉积。

方法三:

[1]熊刚. 机器人铣削加工的误差补偿和力控制方法研究[D]. 上海交通大学, 2019.

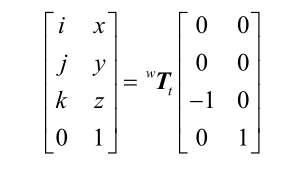
方法四：

计算刀轴向量和 基座标系Z轴之间的变换矩阵

将两个向量之间的变换视为绕某一轴的旋转某一角度的螺旋运动，旋转角为两个向量之间的夹角，而旋转轴则是两个向量之间的叉积。

已知单位向量，将其绕某一轴$\omega$旋转$\theta$，通过使用罗德里格斯公式可以计算其旋转矩阵。
$$
R(\omega,\theta) =I +sin\theta[\omega]+(1-cos\theta)[\omega]^2
$$

方法一：
#使用轴角法求取向量之间的变换矩阵，和上一个函数是一样的方法
def rotation_matrix_from_vectors2(vec2):
    vec1 = [0, 0, 1]
    #规范化两个向量
    a, b = (vec1 / np.linalg.norm(vec1)).reshape(3), (vec2 / np.linalg.norm(vec2)).reshape(3)
    #求两个向量变换的旋转轴
    v = np.cross(a, b)
    s = np.linalg.norm(v)
    v = v / s
    #求旋转角度
    c = np.dot(a, b)
    theta = math.acos(c)
    #使用mr库求取轴角法的旋转矩阵，用的是罗德里格斯公式
    omegaHat = mr.VecToso3(v)
    so3mat = omegaHat * theta
    matrix = mr.MatrixExp3(so3mat)
    #求矩阵对应的欧拉角
    r = R.from_matrix(matrix)
    euler = r.as_euler('ZYX',degrees=True)
    matrix = r.as_matrix()
    return matrix

方法二：本质上都是一样的
def rotation_matrix_from_vectors(vec1,vec2):
    """ Find the rotation matrix that aligns vec1 to vec2
    :param vec1: A 3d "source" vector
    :param vec2: A 3d "destination" vector
    :return mat: A transform matrix (3x3) which when applied to vec1, aligns it with vec2.
    """
    a, b = (vec1 / np.linalg.norm(vec1)).reshape(3), (vec2 / np.linalg.norm(vec2)).reshape(3)
    v = np.cross(a, b)
    c = np.dot(a, b)
    s = np.linalg.norm(v)
    kmat = np.array([[0, -v[2], v[1]], [v[2], 0, -v[0]], [-v[1], v[0], 0]])
    rotation_matrix = np.eye(3) + kmat + kmat.dot(kmat) * ((1 - c) / (s ** 2))
    return rotation_matrix

2、末端姿态对应的欧拉角

末端到基座标的旋转角ABC，是绕动坐标系旋转的ZYX欧拉角，KRC中定义角度A、B和C是绕Z、Y和X的旋转角度，旋转顺序也必须遵从：

1. 绕Z轴旋转角度为A
2. 绕Y轴旋转角度为B
3. 绕X轴旋转角度为C

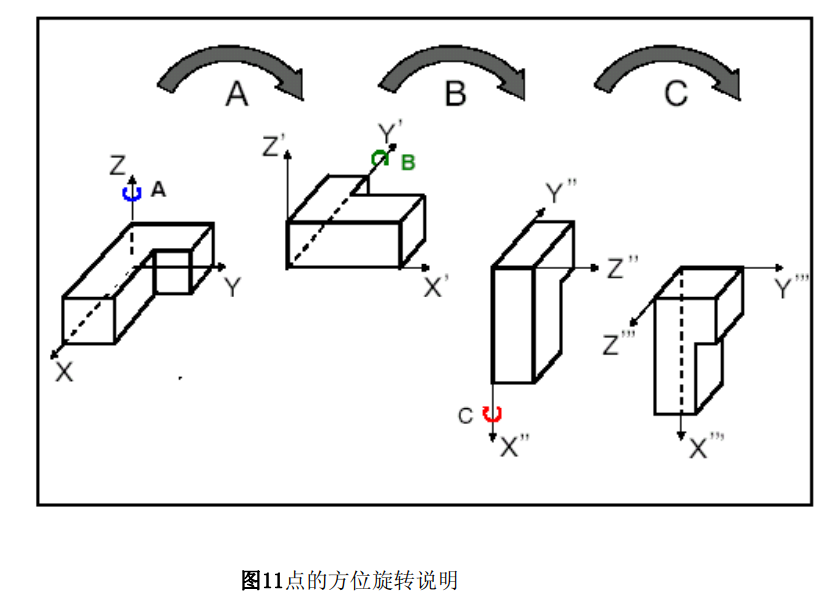
由机器人导论中的方法，对旋转矩阵求逆解
$$
R_{ZYX}=R_Z(\alpha)R_Y(\beta)RX(\gamma)=\begin {bmatrix} r11 & r12 &r13\
r21&r22&r23\
r31&r32&r33\end {bmatrix}\
\beta=Atan2(-r{31},\sqrt{r{11}^2 + r{21}^2})\
\alpha=Atan2(\frac {r{21}}{c\beta},\frac {r{11}}{c\beta})\
\gamma = Atan2(\frac{r{32}}{c\beta},\frac {r{33}}{c\beta})
$$
虽然存在第二个解，但是在上式中取$\beta$的正根以得到单解，满足$-90\le \beta \le 90$，以此获取各种姿态表示法之间一一对应的映射函数。如果等于+-90，解的结果就退化了，这个时候一般取$\alpha = 0$。